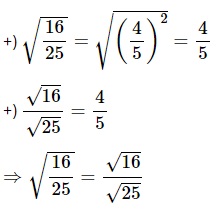Liên hệ giữa phép chia và phép khai phương – Học cùng Itoan

Liên hệ giữa phép chia và phép khai phương là một trong những chuyên đề khó. Bởi vậy, ta cần nắm vững cả kiến thức lý thuyết lẫn kỹ năng làm bài. Để không gây khó khăn cho các em học sinh trong quá trình học tập hay kiểm tra. Itoan sẽ tổng hợp và hệ thống lại những kiến thức lý thuyết nền tảng nhất của liên hệ giữa phép chia và phép khai phương. Đồng thời, Itoan cũng sẽ đưa ra cách giải một số dạng bài tập cơ bản. Chúc các em học tốt!
Định lí liên hệ giữa phép chia và phép khai phương
Với số a không âm và số b dương ta có: √ (a – b) = √ a / √ b
Quy tắc khai phương một thương
Khi chúng ta muốn khai phương một thương a/b mà trong đó a không âm, b dương, thì ta có thể khai phương lần lượt a và b rồi lấy kết quả thứ nhất chia cho kết quả thứ 2.
Quy tắc chia các căn bậc hai
Khi muốn chia các căn bậc hai của số a không âm cho căn bậc hai của số b dương ta có thể chia a cho cho b rồi khai phương kết quả đó.
Chú ý: Một cách tổng quát, với biểu thức Akhông âm và biểu thức B dương ta có √ (A-B) = √ A / √ B
Các dạng bài thường gặp về liên hệ giữa phép chia và phép khai phương
Dạng 1: Thực hiện phép tính
Áp dụng công thức khai phương một tích và khai phương một thương
Với hai biểu thức A, B không âm ta có √ (A.B) = √ A .√ B
Với biểu thức A không âm và biểu thức B dương ta có √ (A/B) = √ A / √ B
Ví dụ:
√ 32 + √ 8 = √ (16.2) + √ (4.2) = √ 16 .√ 2 + √ 4 . √ 2 = 4√ 2 + 2√ 2 = 6 √ 2
Dạng 2: Rút gọn biểu thức – giải bài tập liên hệ giữa phép chia và phép khai phương
Phương pháp:
– Áp dụng công thức khai phương một tích và khai phương một thương
Với hai biểu thức A, B không âm ta có √ (A.B) = √ A .√ B
Với biểu thức A không âm và biểu thức B dương ta có √ (A/B) = √ A / √ B
– Áp dụng hằng đẳng thức √ (A2) = |A|
Ví dụ:
 Dạng 3: Giải phương trình
Dạng 3: Giải phương trình
Phương pháp:
Sử dụng công thức khai phương một tích và khai phương một thương để đưa phương trình đã cho về các dạng quen thuộc:
Liên hệ giữa phép chia và phép khai phương luyện tập
Giải Trả lời câu hỏi Bài 4 trang 16 SGK Toán 9 Tập 1.
Tính và so sánh:
Tính và so sánh: √ (16 – 25) và √ 16/√ 25
Lời giải chi tiết
Trả lời câu hỏi 2 Bài 4 trang 17 SGK Toán 9 Tập 1:
Tính:
- √ (225 – 256)
- √ 0.0196
Trả lời câu hỏi 3 Bài 4 trang 18 SGK Toán 9 Tập 1
Tính:
- √ (999 – 111)
- √ (52 – 117 )
Bí quyết học nhanh nhớ lâu môn Toán
Toán là môn học vô cùng thú vị nếu như các bạn biết phương pháp cũng như bí quyết. Nếu bạn đang đau đầu khi phải ghi nhớ quá nhiều công thức, lẫn lộn giữa các kiến thức với nhau thì cùng Itoan chia sẻ những bí quyết để học Toán nhé.
Chăm chỉ ghi note
Lượng kiến thức hằng ngày mà chúng ta cần phải ghi nhớ là vô cùng nhiều. Cho dù bạn có trí nhớ tốt đến đâu thì cũng không thể ngay lập tức nhớ hết tất cả được. Vì thế, hãy sắm cho mình một quyển sổ nhỏ và luôn mang theo bên người để có thể ngay lập tức ghi lại những thông tin hữu ích.
Ví dụ như khi học đến bài Liên hệ giữa phép chia và phép khai phương chúng ta có thể ghi ngay định lí, quy tắc để cần là có thể thấy và sử dụng ngay lập tức.
Hệ thống lại thông tin
Để kiểm soát được khối lượng kiến thức, hãy hệ thống chúng một cách đầy đủ và chính xác nhất. Hãy sắp xếp và phân loại chúng theo từng chủ đề hoặc thứ tự bài giảng, các kiến thức và thầy cô cung cấp. Như vậy chúng ta sẽ không bị loạn kiến thức và sử dụng các công thức có liên quan đến nhau một cách chính xác và nhanh chóng hơn.
Ghi nhớ bằng hình ảnh
Thay vì viết tràn lan chữ và số ra giấy, bạn hãy sử dụng hình ảnh để ghi nhớ một cách nhanh chóng hơn. Bởi thông qua một hình vẽ, thước phim hay bức tranh là chúng ta đã có thể ghi nhớ được một lượng kiến thức khổng lồ cho bản thân.
Học cách nói và ghi nhớ
Chúng ta sẽ chỉ nhớ được khoảng 20% thông tin khi chúng ta nghe. Nhưng nếu chúng ta là người dạy thì có thể ghi nhớ đến 95% lượng thông tin đó. Bạn hoàn toàn có thể dùng cách này để ghi nhớ thông tin một cách dễ dàng. Đây cũng là cách để chúng ta rèn luyện kỹ năng nói của bản thân.
Vẽ bản đồ tư duy
Bản đồ tư duy không còn là phương pháp quá mới nhưng nó luôn đạt được hiệu quả nhất định. Đây là công cụ trực quan giúp ghi nhớ thông tin một cách hữu hiệu. Việc trình bày bản đồ ra sao tùy thuộc vào sự sáng tạo của mỗi người. Đối với Toán học, chúng ta cũng hoàn toàn có thể sử dụng phương pháp này để ghi nhớ lâu hơn.
Như vậy là phần lý thuyết liên quan đến liên hệ giữa phép chia và phép khai phương đã được Itoan hệ thống lại giúp bạn. Đồng thời chúng tôi cũng đưa ra bí quyết học toán nhanh và nhớ lâu để bạn có thể áp dụng. Muốn tìm hiểu nhiều hơn các kiến thức về môn học này, bạn có thể truy cập vào địa chỉ Itoan

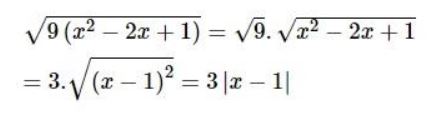 Dạng 3: Giải phương trình
Dạng 3: Giải phương trình