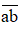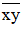Quy tắc đếm – Bài tập & Lời giải Đại số lớp 11

Tổ hợp- xác suất là chuyên đề quan trọng, xuất hiện nhiều trong đề thi THPT quốc gia. Mở đầu phần kiến thức này, chúng ta sẽ cùng tìm hiểu các quy tắc đếm: quy tắc cộng, quy tắc nhân. Bài giảng do iToan biên soạn bám sát theo chương trình sách giáo khoa Đại số 11, giúp các em hiểu bài tốt hơn và làm được các bài tập liên quan.
Lý thuyết cần nắm về Quy tắc đếm
Quy tắc cộng
a. Định nghĩa
Một công việc nào đó có thể được thực hiện theo một trong hai phương án A hoặc B. Nếu phương án A có m cách thực hiện, phương án B có n cách thực hiện và không trùng với bất kì cách nào trong phương án A thì công việc đó có m+n cách thực hiện.
b. Công thức quy tắc cộng
Nếu các tập A1,A2,...,An đôi một rời nhau. Khi đó:
n(A1∪A2∪…∪An)=n(A1)+n(A2)+…+n(An)
Ví dụ: Một trường trung học phổ thông, có 26 học sinh giỏi khối 12, có 43 học sinh giỏi khối 11, có 59 học sinh giỏi khối 10. Vậy nhà trường có bao nhiêu cách chọn 1 học sinh giỏi để đi dự thi trại hè.
Giải
Để chọn một học sinh giỏi đi dự trại hè, ta có thể chọn học sinh giỏi của khối 12, khối 11, hoặc khối 10.
- Chọn 1 học sinh giỏi của khối 12, có 26 cách chọn.
- Chọn 1 học sinh giỏi của khối 11, có 43 cách chọn.
- Chọn 1 học sinh giỏi của khối 10, có 59 cách chọn.
Vậy theo quy tắc cộng có 26+43+59=128 cách chọn thỏa yêu cầu đề bài.
Quy tắc nhân
a. Định nghĩa
Một công việc nào đó có thể bao gồm hai công đoạn A và B. Nếu công đoạn A có m cách thực hiện và ứng với mỗi cách đó có n cách thực hiện công đoạn B thì công việc đó có m.n cách thực hiện.
b. Công thức quy tắc nhân
Nếu các tập A1,A2,...,An đôi một rời nhau. Khi đó:
n(A1∩A2∩…∩An)=n(A1).n(A2)…n(An)
Ví dụ: Bạn B đi học từ nhà đến trường; biết rằng từ nhà đến bến phà có 3 tuyến đường; từ bến phà đến trạm xe buýt có 6 tuyến đường; từ trạm xe buýt có 4 tuyến đường đến trường. Vậy bạn B có bao nhiêu cách chọn tuyến đường đi học.
Giải
Ta chia việc đi học của bạn B thành ba công đoạn sau:
- Công đoạn 1: Bạn B chọn 1 trong 3 con đường để đi từ nhà đến phà, có 3 cách chọn.
- Công đoạn 2: Bạn B chọn 1 trong 6 con đường để đi từ phà đến trạm xe buýt, có 6 cách chọn.
- Công đoạn 3: Bạn B chọn 1 trong 4 con đường để đi từ trạm xe buýt đến trường, có 4 cách chọn.
Theo quy tắc nhân có 3.6.4=72 cách bạn B chọn đường đi học.
Giải bài tập SGK Đại số 11 Quy tắc đếm
Bài 1 (trang 46 SGK Đại số 11):
Từ các chữ số 1, 2, 3, 4 có thể lập được bao nhiêu số tự nhiên gồm:
a.Một chữ số
b.Hai chữ số.
c.Hai chữ số kháu nhau?
Lời giải:
a. Gọi số có 1 chữ số là a
+ a có 4 cách chọn.
Vậy có 4 cách chọn số một chữ số.
b. Gọi số có 2 chữ số cần lập là
+ Chọn a: có 4 cách chọn
+ Chọn b: có 4 cách chọn
Vậy theo quy tắc nhân ta có: 4.4 = 16 (cách lập)
c. Gọi số có 2 chữ số cần lập là
+ Chọn x: có 4 cách chọn
+ Chọn y: có 3 cách chọn (y khác x).
Vậy theo quy tắc nhân ta có: 4.3 = 12 (cách lập).
Bài 2 (trang 46 SGK Đại số 11):
Từ các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên bé hơn 100?
Lời giải:
Các số tự nhiên bé hơn 100 cần lập bao gồm các số có 1 chữ số hoặc số có hai chữ số.
* Trường hợp 1: Số thỏa mãn có 1 chữ số: Có 6 số là: 1, 2, 3, 4, 5, 6.
* Trường hợp 2: Số thỏa mãn có 2 chữ số:
– Chọn chữ số hàng chục: có 6 cách chọn
– Chọn chữ số hàng đơn vị: có 6 cách chọn
⇒ Theo quy tắc nhân: Có 6.6 = 36 số có 2 chữ số được tạo ra từ các số đã cho.
* Theo quy tắc cộng: Có 36 + 6 = 42 số tự nhiên bé hơn 100.được tạo ra từ các chữ số đã cho
Bài 3 (trang 46 SGK Đại số 11):
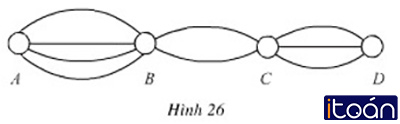
Dưới thành phố A, B, C, D được nối với nhau bởi các con đường như hình dưới:
Hỏi:
a. Có bao nhiêu cách đi từ A đến D mà qua B và C chỉ một lần?
b. Có bao nhiêu cách đi từ A đến D rồi quay lại A?
Lời giải:
a. Việc đi từ A đến D là công việc được hoàn thành bởi ba hành động liên tiếp:
+ Đi từ A đến B: Có 4 con đường.
+ Đi từ B đến C: Có 2 con đường.
+ Đi từ C đến D: Có 3 con đường
⇒ Theo quy tắc nhân: Có 4.3.2 = 24 con đường đi từ A đến D mà chỉ đi qua B và C 1 lần.
b. Có 24 cách đi từ A đến D thì cũng có 24 cách đi từ D đến A.
Việc đi từ A đến D rồi lại quay lại A là công việc được hoàn thành bởi 2 hành động liên tiếp:
+ Đi từ A đến D: Có 24 cách .
+ Đi từ D về A : Có 24 cách
⇒ Theo quy tắc nhân: Có 24.24 = 576 cách đi.
Bài 4 (trang 46 SGK Đại số 11):
Có ba kiểu mặt đồng hồ đeo tay (vuông, tròn, elip) và bốn kiểu dây (kim loại, da, vải và nhựa). Hỏi có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây?
Lời giải:
Việc chọn một chiếc đồng hồ cần thực hiện 2 hành động liên tiếp:
+ Chọn mặt đồng hồ: Có 3 cách chọn.
+ Chọn dây đồng hồ: Có 4 cách chọn.
⇒ Theo quy tắc nhân: Có 3.4 = 12 cách chọn đồng hồ.
Bài tập tự luyện Quy tắc đếm
Các bài tập tự luyện do iToan biên soạn sẽ giúp các em làm quen với tư duy các bài tập trắc nghiệm và ghi nhớ kiến thức tốt hơn!
Phần câu hỏi
Câu 1: Từ các số 1,2,3,4,5,6,7 lập được bao nhiêu số tự nhiên chẵn gồm 4 chữ số khác nhau
A. 360
B. 343
C. 347
D. 523
Câu 2: Cho các số 1,5,6,7 có thể lập được bao nhiêu số tự nhiên có 4 chữ số với các chữ số khác nhau:
A. 12
B. 24
C. 64
D. 256
Câu 3: Cho 6 chữ số 2,3,4,5,6,7 số các số tự nhiên chẵn có 3 chữ số lập thành từ 6 chữ số đó:
A. 36
B. 18
C. 256
D. 108
Câu 4: Có bao nhiêu số tự nhiên có 3 chữ số:
A. 900
B. 901
C. 899
D. 999
Câu 5: Có bao nhiêu số tự nhiên có 3 chữ số đôi một khác nhau lập từ các số 0,2,4,6,8.
A. 60
B. 40
C. 48
D. 10
Phần đáp án
- A 2.B 3.D 4. A 5. C
Lời kết
Các quy tắm đếm là kiến thức nền tảng, giúp các em trong quá trình học tổ hợp, xác suất sau này. Để làm các bài tập quy tắc đếm, các em có thể tìm cách giải nhanh bằng máy tính Casio. Cùng tìm hiểu trên nền tảng học trực tuyến Toppy nhé!
>> Xem thêm các bài giảng khác tại iToan: