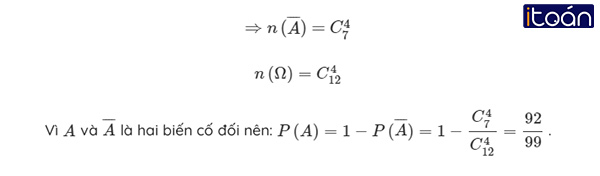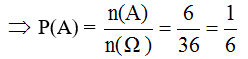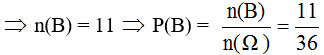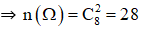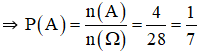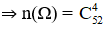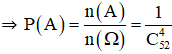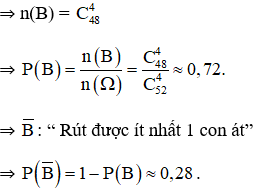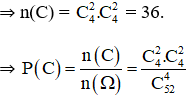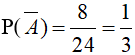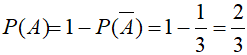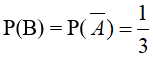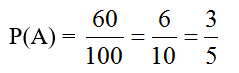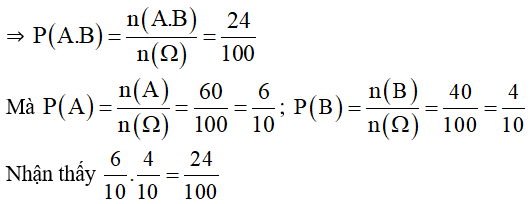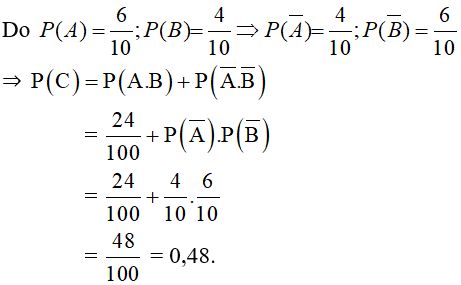Xác suất và biến cố – Giải toán Đại số 11

Bài hôm trước chúng ta đã được học về Phép thử, không gian mẫu và biến cố, trong bài hôm nay, chúng ta sẽ tiếp tục học về Xác suất và biến cố. Bài giảng được biên soạn bởi iToan, bám sát theo chương trình sách giáo khoa Đại số 11, hy vọng sẽ giúp các em trong việc nắm vững lý thuyết và cách làm bài tập. Mời các em học sinh tham khảo!
Bài giảng bao gồm 3 phần
- Tổng hợp lý thuyết cần nắm
- Hướng dẫn giải bài tập SGK Đại số 11
- Các bài tập tự luyện tập
Lý thuyết cần nắm bài Xác suất và biến cố
Định nghĩa cổ điển của xác suất
a. Định nghĩa
Giả sử phép thử T có không gian mẫu Ω là một tập hữu hạn và các kết quả của T là đồng khả năng. Nếu A là một biến cố liên quan với phép thử T và ΩA là một tập hợp các kết quả thuận lợi cho A thì xác suất của A là một số, kí hiệu là P(A), được xác định bởi công thức:
P(A)=|ΩA|/ |Ω|=n(A)/ n(Ω)
Trong đó :
n(A) là số phần tử của A hay cũng là số các kết quả thuận lợi cho biến cố A, còn n(Ω) là số các kết quả có thể xảy ra của phép thử.
b. Ví dụ
Gieo hai đồng xu cân đối một cách độc lập. Tính xác suất để:
A. Cả hai đồng xu đều sấp.
B. Có ít nhất một đồng xu sấp.
C. Có đúng một đồng xu ngửa.
Giải
Ta có không gian mẫu là: Ω{(S;S);(S;N);(N;S);(N;N)}
a. Đặt A: “Cả hai đồng xu đều sấp”
Khi đó: A={(S;S)} , theo định nghĩa ta có
P(A)=|A|/ |Ω|=14
b. Đặt B: “Có ít nhất một đồng xu sấp”.
Khi đó: B={(S;S);(S;N);(N;S)} , nên
P(B)=|B|/ |Ω|=34
c. Đặt C: “Có đúng một đồng xu ngửa”
Khi đó: C={(N;S);(S;N)} , nên
P(C)=|C|/ |Ω|=24=12
Tính chất của xác suất
a. Định lí
Giả sử A và B là các biến cố liên quan đến phép thử có một số hữu hạn kết quả đồng khả năng xuất hiện. Khi đó
(i) P(Ω)=1,P(∅)=0;
(ii) 0≤P(A)≤1
b. Quy tắc cộng xác suất
Nếu A và B xung khắc thì P(A∪B)=P(A)+P(B)
Cho k biến cố A1,A2,...,Ak đôi một xung khắc. Khi đó
P(A1∪A2∪...∪Ak)=P(A1)+P(A2)+...+P(Ak)
c. Hệ quả
Với mọi biến cố A, ta có
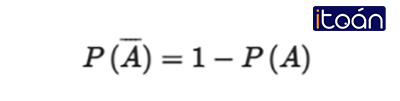
Giải
Gọi A là biến cố “4 quyển sách được chọn phải có ít nhất một quyển toán”. Suy ra biến cố A¯ “4 quyển sách được chọn không có sách toán” có nghĩa 4 quyển sách được chọn chỉ có Vật lý và Hóa học
Các biến cố độc lập, phương pháp nhân xác suất
a. Biến cố độc lập
Hai biến cố A và B được gọi là độc lập với nhau nếu việc xảy ra hay không xảy ra của biến cố này không làm ảnh hưởng tới xác suất xảy ra của biến cố kia.
Tổng quát:
Cho k biến cố A1,A2,...,Ak ; k biến cố này được gọi là độc lập với nhau nếu việc xảy ra hay không xảy ra của mỗi biến cố không làm ảnh hưởng tới xác suất xảy ra của các biến cố còn lại.
b. Quy tắc nhân xác suất
Nếu hai biến cố A và B độc lập với nhau thì
P(AB)=P(A)P(A)...P(Ak)
Quy tắc nhân xác suất cho nhiều biến cố được phát biểu như sau:
P(A1A2...Ak)=P(A1)P(A2)...P(Ak)
c. Ví dụ
Gieo hai đồng xu A và B một cách độc lập. Đồng xu A chế tạo cân đối. Đồng xu B chế tạo không cân đối nên xác suất xuất hiện mặt sấp gấp 3 lần xác suất xuất hiện mặt ngửa. Tính xác suất để khi gieo 2 đồng xu một lần thì cả hai đều ngửa.
Giải
- Gọi X là biến cố ” Đồng xu A xuất hiện mặt ngửa “.
- Gọi Y là biến cố ” Đồng xu B xuất hiện mặt ngửa “.
Vì đồng xu A chế tạo cân đối nên P(X)=12
Theo giả thuyết thì xác suất xuất hiện mặt sấp của đồng xu B gấp 3 lần xác suất xuất hiện mặt ngửa do đó P(Y)=14
Biến cố cần tính cả hai đồng xu đều xuất hiện mặt ngửa là X.Y. Vì X, Y là hai biến cố độc lập nên P(X.Y)=P(X).P(Y)=12.14=18
Giải bài tập SGK Đại số 11 Xác suất và biến cố
Bài 1 (trang 74 SGK Đại số 11):
Gieo ngẫu nhien một con súc sắc cân đối và đồng chất hai lần.
a.Hãy mô tả không gian mẫu.
b.Xác định các biến cố sau.
A: “Tổng số chấm xuất hiện trong hai lần gieo không bé hơn 10”
B: “Mặt 5 chấm xuất hiện ít nhất một lần”.
c.Tính P(A), P(B).
Lời giải:
a. Không gian mẫu gồm 36 kết quả đồng khả năng xuất hiện, được mô tả như sau:
Ta có: Ω = {(i, j) | 1 ≤ i , j ≤ 6}, trong đó i, j lần lượt là số chấm xuất hiện trong lần gieo thứ nhất và thứ hai, n(Ω) = 36.
b. A = {(4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6)} ⇒ n(A) = 6
B = {(1, 5), (2, 5), (3, 5), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 5)}
Bài 2 (trang 74 SGK Đại số 11):
Có 4 tấm bìa được đánh số từ 1 đến 4. Rút ngẫu nhiên 3 tấm.
a. Hãy mô tả không gian mẫu.
b. Xác định các biến cố sau:
A: “Tổng các số trên 3 tấm bìa bằng 8”
B: “Các số trên 3 tấm bìa là ba số tự nhiên liên tiếp”
c.Tính P(A), P(B).
Lời giải:
a.Không gian mẫu gồm 4 phần tử:
Ω = {(1, 2, 3);(1,2,4);(2,3,4);(1,3,4)} ⇒ n(Ω)=4
Bài 3 (trang 74 SGK Đại số 11):
Một người chọn ngẫu nhiên hai chiếc giày từ bốn đôi giày cỡ khác nhau. Tính xác suất để hai chiếc chọn được tạo thành một đôi.
Lời giải:
Không gian mẫu là kết quả của việc chọn ngẫu nhiên 2 chiếc giày trong số 8 chiếc giày.
A: “ Chọn được 2 chiếc tạo thành một đôi”
⇒ n(A) = 4 (Vì có 4 đôi).
Bài 4 (trang 74 SGK Đại số 11):
Gieo một con súc sắc cân đối và đồng nhất. giả sử con súc sắc xuất hiện mặt b chấm. Xét phương trình x2 + bx + 2 = 0. Tính xác suất sao cho:
a. Phương trình có nghiệm
b. Phương trình vô nghiệm
c. Phương tring có nghiệm nguyên.
Lời giải:
Không gian mẫu khi gieo con súc sắc cân đối và đồng chất:
Ω = {1, 2, 3, 4, 5, 6}
⇒ n(Ω) = 6
Đặt A: “con súc sắc xuất hiện mặt b chấm”;
Xét : x2 + bx + 2 = 0 (1)
Δ = b2 – 8
a. Phương trình (1) có nghiệm
⇔ Δ ≥ 0 ⇔ b ≥ 2√2
⇒ b ∈ {3; 4; 5; 6}.
⇒ A = {3, 4, 5, 6}
⇒ n(A) = 4
b. (1) vô nghiệm
⇔ Δ < 0 ⇔ b ≤ 2√2
⇒ b ∈ {1; 2}
⇒ A = {1, 2}
⇒ n(A) = 2
c. phương trình (1) có nghiệm
⇔ b ∈ {3; 4; 5; 6}.
Thử các giá trị của b ta thấy chỉ có b = 3 phương trình cho nghiệm nguyên.
⇒ A = {3}
⇒ n(A) = 1
Bài 5 (trang 74 SGK Đại số 11):
Từ cỗ bài tú lơ khơ 52 con, rút ngẫu nhiên cùng một lúc bốn con. Tính xác suất sao cho:
a. Cả bốn con đều là át.
b. Được ít nhất là một con át.
c. Được hai con át và hai con K
Lời giải:
Không gian mẫu là kết quả của việc chọn ngẫu nhiên 4 con trong số 52 con
a. Đặt A : « Cả 4 con lấy ra đều là át »
⇒ n(A) = 1
b. + B : « Không có con át nào trong 4 con khi lấy ra »
⇒ B là kết quả của việc chọn ngẫu nhiên 4 con trong số 48 con còn lại
c. C: “Rút được 2 con át và 2 con K”.
Bài 6 (trang 74 SGK Đại số 11):
Hai bạn nam và hai bạn nữ được xếp ngồi ngẫu nhiên vào bốn ghế xếp thành hai dãy đối diện nhau. Tính xác suất sao cho:
a. Nam, nữ ngồi đối diện nhau.
b. Nữ ngồi đối diện nhau.
Lời giải:
a) Không gian mẫu là kết quả của việc sắp xếp bốn bạn vào 4 vị trí
⇒n( Ω) = 4! = 24.
Gọi A: “ Sắp xếp nam, nữ ngồi đối diện nhau”.
=> Biến cố đối A− : “ Nam ngồi đối diện nam, nữ ngồi đối diện nữ”
+ Ta tính P(A−):
Có 4 chỗ để cho bạn nữ thứ nhất chọn.
Có 1 cách chọn cho bạn nữ thứ hai ( đối diện với bạn nữ thứ nhất).
Sau khi hai bạn nữ đã được chọn ( ngồi đối diện nhau) thì còn lại 2 chỗ đối diện nhau để xếp 2 bạn nam và có 2! Cách xếp 2 bạn nam này.
Theo quy tắc nhân có: 4.1.2! = 8 cách xếp chỗ sao cho nam ngồi đối diện nam, nữ ngồi đối diện nữ
Do đó,
Suy ra, xác suất biến cố A là:
b) Theo phần trên xác suất để nữ ngồi đối diện nhau ( khi đó hai nam cũng ngồi đối diện nhau) là:
Bài 7(trang 75 SGK Đại số 11):
Có hai hộp chứa các quả cầu. Hộp thứ nhất chứa 6 quả trắng, 4 quả đen. Hộp thứ hai chứa 4 quả trắng, 6 quả đen. Từ mỗi hộp lấy ngẫu nhiên một quả. Kí hiệu:
A là biến cố: “Qủa lấy từ hộp thứ nhất trắng”
B là biến cố: “Qủa lấy từ hộp thứ hai trắng”
a. Xem xét A và B có độc lập không?
b. Tính xác suất sao cho hai quả cầu lấy ra cùng màu.
c. Tính xác suất sao cho hai quả cầu lấy ra khác màu.
Lời giải:
a) Không gian mẫu là kết quả của việc lấy ngẫu nhiên 1 quả cầu ở hộp thứ nhất và một quả cầu ở hộp thứ hai
+ Có 10 cách lấy 1 quả cầu bất kì ở hộp 1 và có 10 cách lấy 1 quả cầu bất kì ở hộp 2. Nên số phần tử của không gian mẫu là;
⇒ n(Ω) = 10.10 = 100.
A: “ Quả cầu lấy từ hộp thứ nhất trắng”
⇒ Có 6 cách lấy quả cầu màu trắng ở hộp A và 10 cách lấy quả cầu ở hộp B
⇒ n(A) = 6.10 = 60.
B: “Quả cầu lấy từ hộp thứ hai trắng”
⇒ Có 4 cách lấy quả cầu màu trắng ở hộp B và 10 cách lấy quả cầu ở hộp A
⇒ n(B) = 4.10 = 40.
A.B: “Cả hai quả cầu lấy ra đều trắng”
⇒ Có 6 cách lấy quả cầu màu trắng ở hộp A và 4 cách lấy quả cầu màu trắng ở hộp B
⇒ n(A.B) = 6.4 = 24.
hay P(A.B) = P(A).P(B)
⇒ A và B là biến cố độc lập.
>> Xem thêm các bài giảng khác tại Toppy.
b) Gọi C: “Hai quả cầu lấy ra cùng màu”.
Ta có: A− : “Quả cầu lấy ra từ hộp thứ nhất màu đen”
B− : “ Quả cầu lấy ra từ hộp thứ hai màu đen”
⇒A−.B− : “Cả hai quả cầu lấy ra đều màu đen”
Nhận thấy A.B và A−.B− xung khắc (Vì không thể cùng lúc xảy ra hai trường hợp 2 quả cầu lấy ra cùng trắng và cùng đen)
Và C=(A.B)∪(A−.B−)
c) C− : “Hai quả cầu lấy ra khác màu”
⇒ P(C− )=1-P(C)=1-0,48=0,52
Bài tập tự luyện Xác suất và biến cố
Câu 1: Cho A là một biến cố liên quan phép thử T. Mệnh đề nào sau đây là mệnh đề đúng ?
A. P(A) là số lớn hơn 0.
B. P(A)=1−P(A¯).
C. P(A)=0⇔A=Ω.
D. P(A) là số nhỏ hơn 1.
Câu 2: Gieo đồng tiền 5 lần cân đối và đồng chất. Xác suất để được ít nhất một lần xuất hiện mặt sấp là:
A. 31/ 32.
B. 21/ 32
C. 11/ 32.
D. 1/ 32.
Câu 3: Một con súc sắc cân đối đồng chất được gieo 5 lần. Xác suất để tổng số chấm ở hai lần gieo đầu bằng số chấm ở lần gieo thứ ba:
A. 10/ 216
B. 15/ 216
C. 16/ 216.
D. 12/ 216.
Câu 4: Gieo hai con súc xắc cân đối và đồng chất. Xác suất để hiệu số chấm trên mặt xuất hiện của hai con súc xắc bằng 2 là:
A. 1/12
B. 1/9
C. 2/9
D. 5/36
Câu 5: Gieo một con súc sắc cân đối và đồng chất hai lần. Xác suất để tổng số chấm xuất hiện là một số chia hết cho 5 là:
A. 4/36
B. 6/36
C. 5/36
D. 7/36
Phần đáp án
1.B 2.A 3.B 4.B 5.D
Lời kết
Bài giảng: Xác suất và biến cố kết thúc tại đây! Các em nên tự luyện tập thật nhiều các bài tập trắc nghiệm tại Toppy. Toppy là nền tảng học trực tuyến, giúp các em tổng hợp và nâng cao kiến thức của mình.
Chặng đường học tập có nhiều khó khăn và thử thách, hãy đồng hành cùng Toppy em nhé!
>> Xem thêm:
- Lý thuyết & Bài tập: Phương trình tích
- Biểu thức chứa ba chữ
- Bảng phân bố tần số và tần suất- Đại số 10