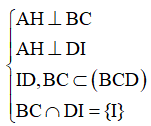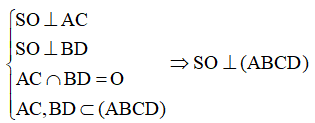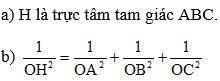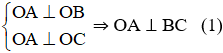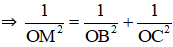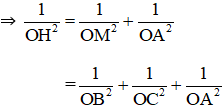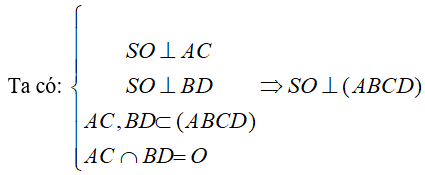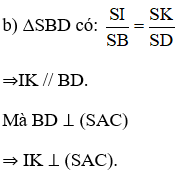Đường thẳng vuông góc với mặt phẳng – Toán học 11

Bài học hôm nay sẽ dẫn chúng ta đến một chủ điểm mới :” Đường thẳng vuông góc với mặt phẳng ” . Vậy khi nào đường thẳng vuông góc với mặt phẳng và tính chất của chúng là gì ? Để giải đáp mọi thắc mắc của các bạn thì chúng ta cùng nhau bước vào bài học hôm nay với Itoan ngay nhé !
Mục tiêu bài học : Đường thẳng vuông góc với mặt phẳng
Sau bài học , các bạn sẽ củng cố thêm cho bản thân những kiến thức sau đây :
- Khái niệm và tính chất của đường thẳng khi vuông góc với mặt phẳng
- Bài tập liên qua đến những kiến thức đã học trên
Kiến thức cơ bản của bài học : Đường thẳng vuông góc với mặt phẳng
Sau đây cùng Itoan đi tìm hiểu những kiến thức cơ bản của bài học nhé !
1. Định nghĩa
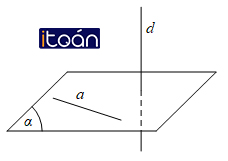
Ta có được nhận xét như sau :Đường thẳng d được gọi là vuông góc với mặt phẳng (α) nếu d vuông góc với mọi đường thẳng a nằm trong mặt phẳng (α).
Kí hiệu d ⊥ (α).
2. Điều kiện để đường thẳng vuông góc với mặt phẳng
Định lí
Ta có định lý sau đây : Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
Hệ quả
Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì nó cũng vuông góc với cạnh thứ ba của tam giác đó.
3. Tính chất
Tính chất 1
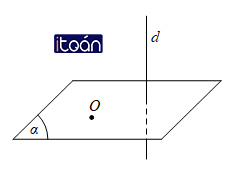
Ta nhận thấy rằng : Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
Mặt phẳng trung trực của một đoạn thẳng
Chúng ta có thể gọi mặt phẳng đi qua trung điểm I của đoạn thẳng AB và vuông góc với AB là mặt phẳng trung trực của đoạn thẳng AB.
Tính chất 2
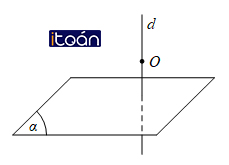
Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
4. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng.
Tính chất 1
Khi ta cho hai đường thẳng song song. Mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
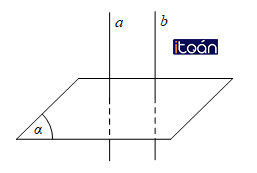
Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
Tính chất 2
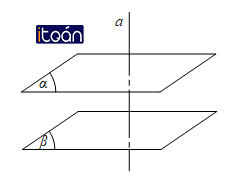
Cho hai mặt phẳng song song. Đường thẳng nào vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.
Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
Tính chất 3
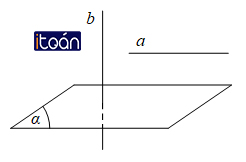
Cho đường thẳng a và mặt phẳng (α) song song với nhau. Đường thẳng nào vuông góc với (α) thì cũng vuông góc với a.
Nếu một đường thẳng và một mặt phẳng (không chứa đường thẳng đó) cùng vuông góc với một đường thẳng khác thì chúng song song với nhau.
5. Định lí ba đường vuông góc
Định nghĩa
Phép chiếu song song lên mặt phẳng (P) theo phương vuông góc tới mặt phẳng (P) gọi là phép chiếu vuông góc lên mặt phẳng (P).
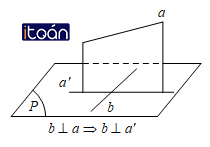
Định lí (Định lí 3 đường vuông góc)
Cho đường thẳng a không vuông góc với mặt phẳng (P) và đường thẳng b nằm trong mặt phẳng (P). Khi đó điều kiện cần và đủ để b vuông góc với a là b vuông góc với hình chiếu a’ của a trên (P).
6. Góc giữa đường thẳng và mặt phẳng
Định nghĩa
Nếu đường thẳng a ⊥ (P) thì ta nói góc giữa đường thẳng a và mặt phẳng (P) bằng 90°.
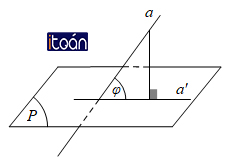
Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì góc giữa a và hình chiếu a’ của nó trên (P) gọi là góc giữa đường thẳng a và mặt phẳng (P).
Chú ý: Nếu φ là góc giữa đường thẳng d và mặt phẳng (α) thì ta luôn có 0° ≤ φ ≤ 90°.
Hướng dẫn giải bài tập toán SGK lớp 11 bài học : Đường thẳng vuông góc với mặt phẳng
Để kiểm tra cũng như gợi nhớ lại những kiến thức vừa học , chúng ta sẽ cùng đi giải một số bài tập sau đây :
Bài 1 :
Chúng ta có câu hỏi lý thuyết sau đây : Cho mặt phẳng (α) và hai đường thẳng a, b. Các mệnh đề sau đây đúng hay sai?
a) Nếu a // (α), b ⊥(α) thì a ⊥b.
b) Nếu a // (α), b ⊥a thì b ⊥(α).
c) Nếu a // (α), b // (α) thì b // a.
d) Nếu a ⊥(α), b ⊥a thì b ⊥(α).
Lời giải:
a) Đúng
b) Sai
c) Sai
d) Sai
Bài 2 :
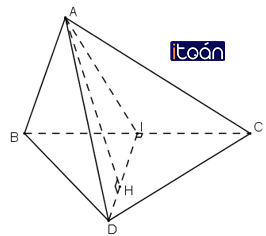
Những dữ liệu mà ta có như sau : Cho tứ diện ABCD có hai mặt ABC và BCD là hai tam giác cân có chung đáy BC. Gọi I là trung điểm của cạnh BC.
a) Chứng minh rằng BC vuông góc với mặt phẳng (ADI)
b) Gọi AH là đường cao của tam giác ADI, chứng minh rằng AH vuông góc với mặt phẳng (BCD).
a) Tam giác ABC cân tại A có AI là đường trung tuyến nên đồng thời là đường cao:
AI ⊥ BC
+) Tương tự, tam giác BCD cân tại D có DI là đường trung tuyến nên đồng thời là đường cao:
DI ⊥ BC
+) Ta có:
Bài 3 :
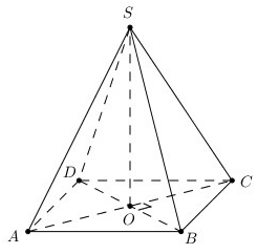
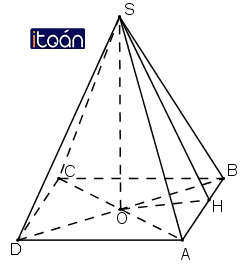
Cùng đọc đề bài và giải bài toán sau đây : Cho hình chóp S.ABCD có đáy là hình thoi ABCD tâm O và có SA = SB = SC = SD. Chứng minh rằng:
a) Đường thẳng SO vuông góc với mặt phẳng (ABCD)
b) Đường thẳng AC vuông góc với mặt phẳng (SBD) và đường thẳng BD vuông góc với mặt phẳng (SAC).
Lời giải:
Bài 4 :
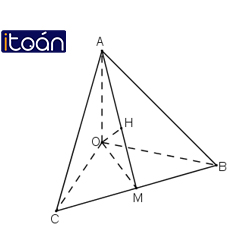
Ta có những dữ liệu sau đây : Cho tứ diện OABC có ba cạnh OA, OB và OC đôi một vuông góc. Gọi H là chân đường vuông góc hạ từ O tới mặt phẳng (ABC). Chứng minh rằng :
a) Ta có:
Do H là chân đường vuông góc hạ từ O tới mặt phẳng (ABC) nên:
OH ⊥ (ABC) ⇒ OH ⊥ BC (2)
Mà OA; OH ⊂ (OAH); OA ∩ OH = O (3)
Từ (1); (2) và (3) ⇒ BC ⊥ (OAH)
⇒ BC ⊥ AH
Chứng minh tương tự ta có: AC ⊥ BH
⇒ H là trực tâm ΔABC.
b) Gọi M = AH ∩ BC.
+ BC ⊥ (OAH) ⇒ BC ⊥ OM.
ΔOBC vuông tại O có đường cao OM
+ OA ⊥ (OBC) ⇒ OA ⊥ OM ⇒ ΔOAM vuông tại O.
OH ⊥ (ABC) ⇒ OH ⊥ AM.
Bài 5 :
Bài học sau đây gồm những dữ liệu sau : Trên mặt phẳng (α) cho hình bình hành ABCD tâm O. Gọi S là một điểm nằm ngoài mặt phẳng (α) sao cho SA = SC, SB = SD. Chứng minh rằng:
a) SO ⊥(α)
b) Nếu trong mặt phẳng (SAB) kẻ SH vuông góc với AB tại H thì AB vuông góc với mặt phẳng (SOH).
Lời giải:
a)
+ Do ABCD là hình bình hành có tâm O- giao điểm hai đường chéo
=> O là trung điểm AC và BD( tính chất hình bình hành)
* Xét tam giác SAC có SA= SC nên tam giác SAC cân tại S
Lại có SO là đường trung tuyến nên đồng thời là đường cao: SO ⊥ AC
+ Tương tự, tam giác SBD cân tại S có SO là đường trung tuyến nên đồng thời là đường cao:
b) SO ⊥ (α) ⇒ SO ⊥ AB.
Lại có: SH ⊥ AB;
SO, SH ⊂ (SOH) và SO ∩ SH
⇒ AB ⊥ (SOH).
Bài 6 :
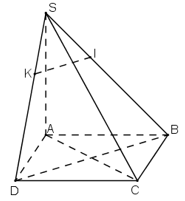
Cùng phân tích bài học với những dữ liệu sau : Cho hình chóp S.ABCD có đáy là hình thoi ABCD và có cạnh SA vuông góc với mặt phẳng (ABCD). Gọi I và K là hai điểm lần lượt lấy trên hai cạnh SB và SD sao cho SI/SB = SK/SD . Chứng minh:
a) BD ⊥ SC
b) IK ⊥mp(SAC)
Lời giải:
Chú ý : Còn hai bài 7 và 8 , các bạn ứng dụng các kiến thức đã học và , tham khảo các giải các bài trên để hoàn thiện
Lời kết :
Bài học sẽ cung cấp cho các bạn các kiến thức cũng như các cách giải các bài tập Toán liên quan đến chủ đề : Đường thẳng vuông góc với mặt phẳng . Itoan mong rẳng với bài giảng trên đã giúp các bạn hiểu bài và áp dựng vào làm các bài tập tương tự . Các bạn tham khảo thêm tại : https://www.toppy.vn/
Chúc các bạn học tốt !
Xem thêm :
- Khoảng cách – Hướng dẫn học tốt Hình học lớp 11 – itoan
- Hai đường thẳng chéo nhau và hai đường thẳng song song – Toán 11
- Từ vuông góc đến song song
- Phương trình đường thẳng trong không gian