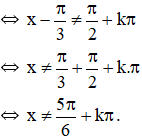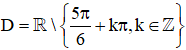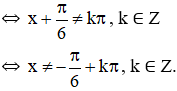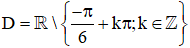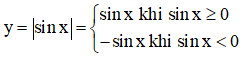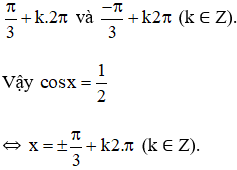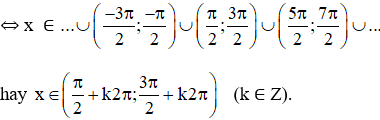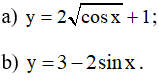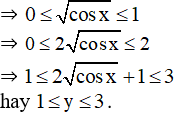Hàm số lượng giác – Bài tập & Lời giải Toán lớp 11

Mở đầu chương trình Toán Đại số 11, chúng ta sẽ cùng tìm hiểu về một nội dung kiến thức mới: Hàm số lương giác. Chắc hẳn qua chương trình Toán Trung học cơ sở, các em đã quen thuộc với các đại lượng: sin, cos, tan.. Trong bài học này, chúng ta sẽ tìm hiểu về tính chất cũng như cách vẽ đồ thị của các hàm số đó. Cùng học với iToan nhé!

Nội dung bài học

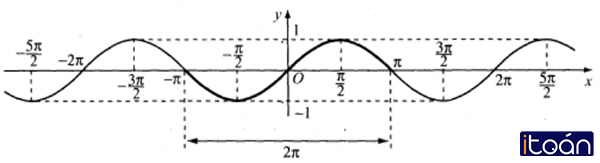
Hàm số y= sin x

• Tập xác định: D=R
• Tập giác trị: [−1;1], tức là −1≤sinx≤1∀x∈R
• Hàm số đồng biến trên mỗi khoảng (−π/2+k2π; π/2+k2π), nghịch biến trên mỗi khoảng (π/2+k2π; 3π/2+k2π).
• Hàm số y=sinx là hàm số lẻ nên đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng.
• Hàm số y=sinx là hàm số tuần hoàn với chu kì T=2π.
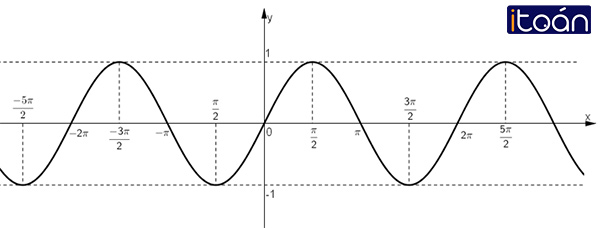
• Đồ thị hàm số y=sinx.

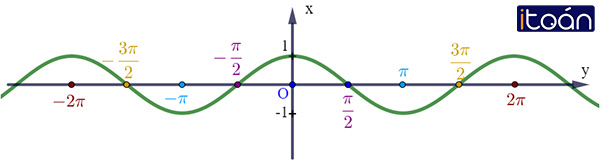
Hàm số y = cos x

• Tập xác định: D=R
• Tập giác trị: [−1;1], tức là −1≤cosx≤1∀x∈R
• Hàm số y=cosx nghịch biến trên mỗi khoảng (k2π;π+k2π), đồng biến trên mỗi khoảng (−π+k2π;k2π).
• Hàm số y=cosx là hàm số chẵn nên đồ thị hàm số nhận trục Oy làm trục đối xứng.
• Hàm số y=cosx là hàm số tuần hoàn với chu kì T=2π.
• Đồ thị hàm số y=cosx.
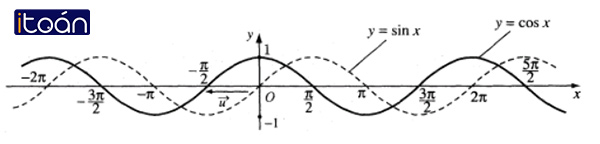
• Đồ thị hàm số y=cos⁡x bằng cách tịnh tiến đồ thị hàm số y=sinx theo véc tơ v⃗ =(−π/2;0).

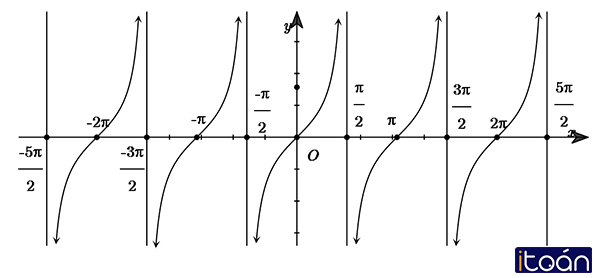
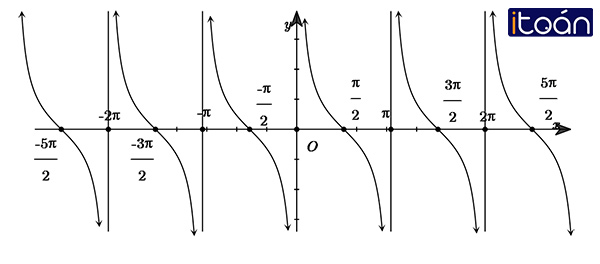
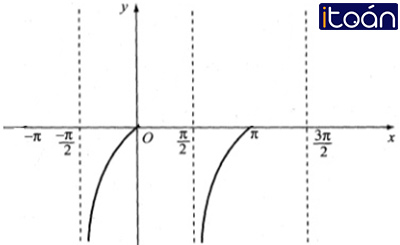
Hàm số y= tan x

• Tập xác định : D = R∖{π/2+kπ,k∈Z}
• Tập giá trị: R
• Là hàm số lẻ
• Là hàm số tuần hoàn với chu kì T=π
• Hàm đồng biến trên mỗi khoảng (−π/2+kπ; π/2+kπ)
• Đồ thị nhận mỗi đường thẳng x=π/2+kπ,k∈Z làm một đường tiệm cận.
• Đồ thị:

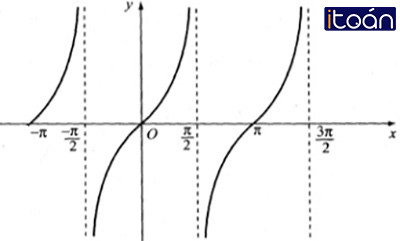
Hàm số y= cot x

• Tập xác định : D = R∖{kπ,k∈Z}
• Tập giá trị: R
• Là hàm số lẻ
• Là hàm số tuần hoàn với chu kì T=π
• Hàm nghịch biến trên mỗi khoảng (kπ;π+kπ)
• Đồ thị nhận mỗi đường thẳng x=kπ,k∈Z làm một đường tiệm cận.
• Đồ thị:

Giải bài tập SGK trang 17 Hàm số lượng giác

Bài 1 (trang 17 SGK Đại số 11):

Hãy xác định giá trị của x trên đoạn [- π ; 3π/2] để hàm số y = tan x:

a. Nhận giá trị bằng 0

b. Nhận giá trị bằng 1

c. Nhận giá trị dương

d. Nhận giá trị âm

Lời giải:

Quan sát đồ thị hàm số y = tan x trên đoạn [-π; 3π/2].

a. tan x = 0 tại các giá trị x = -π; 0; π.

(Các điểm trục hoành cắt đồ thị hàm số y = tanx).

b. tan x = 1 tại các giá trị x = -3π/4; π/4; 5π/4.

c. tan x > 0 với x ∈ (-π; -π/2) ∪ (0; π/2) ∪ (π; 3π/2).

d. tan x < 0 khi x ∈ [-π/2; 0) ∪ [π/2; π)

Bài 2 (trang 17 SGK Đại số 11): 

Tìm tập xác định của hàm số:

Lời giải:

a) Hàm số 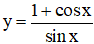 xác định

⇔ sin x ≠ 0

⇔ x ≠ k.π (k ∈ Z).

Tập xác định của hàm số là D = R \{kπ, k ∈ Z}.

b) Hàm số 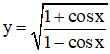 xác định

Do đó (1) ⇔ 1 – cos x ≠ 0 ⇔ cos x ≠ 1 ⇔ x ≠ k.2π.

Vậy tập xác định của hàm số là D = R \ {k.2π, k ∈ Z}.

c) Hàm số 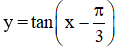 xác định

Vậy tập xác định của hàm số là 

d) Hàm số 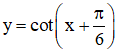 xác định

Vậy tập xác định của hàm số là 

Bài 3 (trang 17 SGK Đại số 11): 

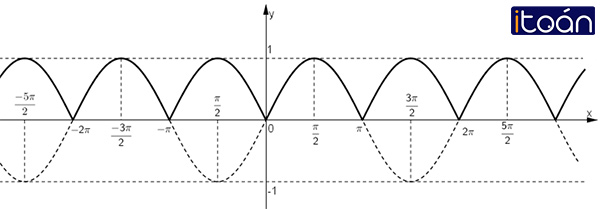
Dựa vào đồ thị của hàm số y = sin x, vẽ đồ thị của hàm số y = | sin x|

Lời giải:

+ Đồ thị hàm số y = sin x.

+ Ta có:

Vậy từ đồ thị hàm số y = sin x ta có thể suy ra đồ thị hàm số y = |sin x| bằng cách:

– Giữ nguyên phần đồ thị nằm phía trên trục hoành (sin x > 0).

– Lấy đối xứng phần đồ thị nằm phía dưới trục hoành qua trục hoành.

Ta được đồ thị hàm số y = |sin x| là phần nét liền.

Bài 4 (trang 17 SGK Đại số 11): 

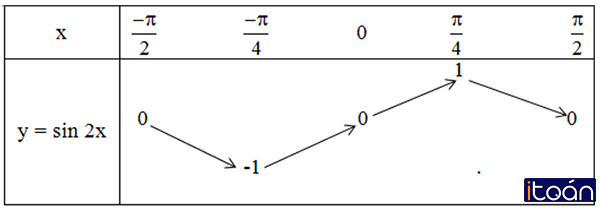
Chứng minh rằng sin 2(x + kπ) = sin 2x với mọi số nguyên k. Từ đó vẽ đồ thị hàm số y = sin 2x

Lời giải:

+ sin 2x (x + kπ) = sin (2x + k2π) = sin 2x, (k ∈ Z)

(Do hàm số y = sin x có chu kì 2π).

⇒ Hàm số y = sin 2x tuần hoàn với chu kì π.

+ Hàm số y = sin 2x là hàm số tuần hoàn với chu kì π và là hàm số lẻ.

Bảng biến thiên hàm số y = sin 2x trên [-π/2; π/2]

Đồ thị hàm số y = sin 2x.

Bài 5 (trang 18 SGK Đại số 11): 

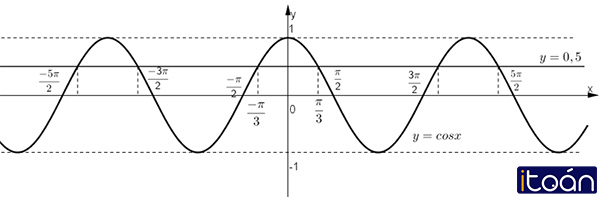
Dựa vào đồ thị hàm số y = cos x, tìm các giá trị của x để cos x = 1/2

Lời giải:

+ Vẽ đồ thị hàm số y = cos x.

+ Vẽ đường thẳng 

+ Xác định hoành độ các giao điểm.

Ta thấy đường thẳng 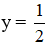 cắt đồ thị hàm số y = cos x tại các điểm có hoành độ

Bài 6 (trang 18 SGK Đại số 11):

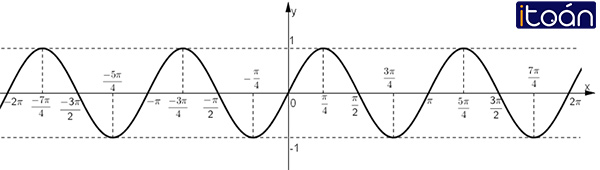
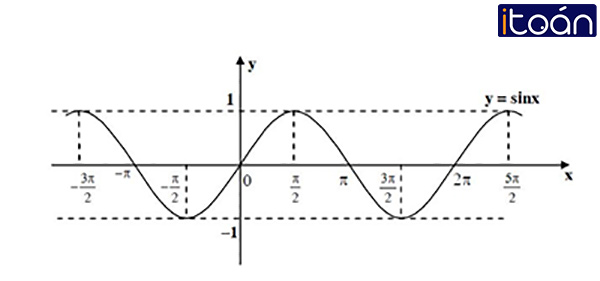
Dựa trên đồ thị hàm số y = sin x, tìm các khoảng giá trị của x để hàm số đó nhận giá trị dương.

Lời giải:

Đồ thị hàm số y = sin x:

Dựa vào đồ thị hàm số y = sin x ta thấy

y = sin x > 0

⇔ x ∈ (-2π; -π) ∪ (0; π) ∪ (2π; 3π) ∪…

hay x ∈ (k2π; π + k2π) với k ∈ Z.

Bài 7 (trang 18 SGK Đại số 11): 

Dựa vào đồ thị hàm số y = cos x, tìm các khoảng giá trị của x để hàm số đó nhận giá trị âm.

Lời giải:

Dựa vào đồ thị hàm số y = cos x ta thấy

y = cos x < 0

Bài 8 (trang 18 SGK Đại số 11): 

Tìm giá trị lớn nhất của các hàm số:

Lời giải:

a) Ta có:

Vậy hàm số đạt giá trị lớn nhất bằng 3.

b) Ta có: -1 ≤ sin x ≤ 1

⇒ -2 ≤ -2sin x ≤ 2

⇒ 1 ≤ 3 – 2sin x ≤ 5

hay 1 ≤ y ≤ 5.

Vậy hàm số đạt giá trị lớn nhất bằng 5.

Bài tập tự luyện Hàm số lượng giác

Các bài tập tự luyện sẽ giúp em ghi nhớ và nâng cao kiến thức!

Phần câu hỏi

Câu 1: Tâp xác định của hàm số y=1/ (sinx−cosx) là

A. x≠kπ.

B. x≠k2π.

C. x≠π/2+kπ.

D. x≠π/4+kπ.

Câu 2: Tập xác định của hàm số y=cotx/ (cosx−1) là

A. R∖{kπ/2,k∈Z}

B. R∖{π/ 2+kπ,k∈Z}

C. R\ {kπ,k∈Z}

D. R

Câu 3: Tập xác định của hàm số y=tan2x

A. x≠−π/4+kπ/2

B. x≠π/2+kπ

C. x≠π/4+kπ/2

D. x≠π/4+kπ

Câu 4: Tập xác định cùa hàm số y=(1−2cosx)/ (sin3x−sinx )là

A. R∖{kπ;π/4+kπ,k=Z}

B. R∖{π/4+kπ/2,k∈Z}.

C. R∪{kπ,k∈2}.

D. R∖{kπ;π/ 4+kπ/ 2,k=Z}

Câu 5:

.

Phần đáp án

1.D     2.C     3.C     4.D    5.A

Lời kết

Vậy là chúng ta đã học xong bài đầu tiên của chương trình Toán 11. Toán 11 bao gồm nhiều phần kiến thức hoàn toàn mới, làm nền tảng cho kì thi THP quốc gia. Để ôn luyện và nắm chăc kiến thức ngày từ bây giờ, các em có thể tham gia các khóa học của Toppy. Toppy với đội ngũ giáo viên tận tụy cùng kho tàng kiến thức khổng lồ theo từng chủ đề, bám sát chương trình sách giáo khoa, chắc chắn sẽ giúp em tự tin làm chủ kiến thức.

>> Xem thêm nhiều bài giảng khác tại iToan:

• Tỉ số lượng giác của góc nhọn
• Bảng lượng giác
• Tổng hợp ý thuyết về hàm số
• Kiến thức cần nhớ về hàm số bậc hai