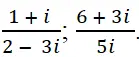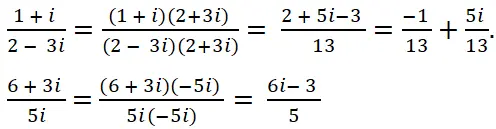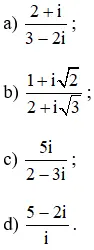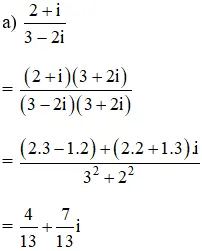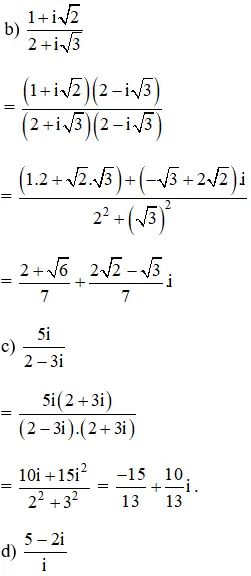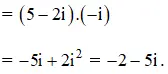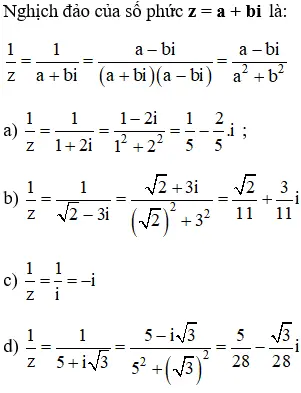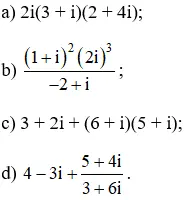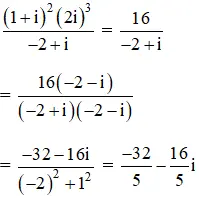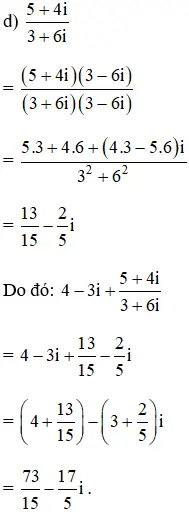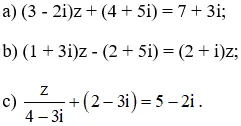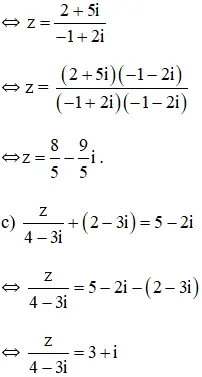Phép chia số phức – Cùng itoan chinh phục giải tích 12

Hướng dẫn giải chi tiết bài tập: Phép chia số phức – SGK Giải tích lớp 12. Nhằm cung cấp một nguồn tài liệu giúp học sinh tham khảo, ôn luyện và nắm vững hơn kiến thức trên lớp, chúng tôi mang đến cho các bạn lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa Đại số và Giải tích Giải tích lớp 12. Bài giảng này có tổng hợp lý thuyết cần nhớ và hướng dẫn giải bài tập sách giáo khoa, mong các bạn sẽ học tập tốt hơn!
Mục tiêu của bài học Phép chia số phức
Kiến thức bài học hôm nay có đôi chút liên quan đến những bài học trước, các bạn cố gắng học tốt những bài học trước và đặt ra mục tiêu cụ thể cho bài học hôm nay nhé!
- Học sinh phải nắm được nội dung và thực hiện được các phép tính về tổng và tích của hai số phức liên hợp.
- Nội dung và các tính chất của phép chia hai số phức .
Lý thuyết bài học Phép chia số phức
Dưới đây là một số phần kiến thức quan trọng cơ bản cô đã biên soạn cho bài học hôm nay, các bạn nhớ học bài kỹ trước khi làm bài tập nhé!
1. Tổng và tích của hai số phức liên hợp
Ví dụ 1: Cho z=2+3i Ta có:
z+z¯¯¯=(2+3i)+(2−3i)=4
z.z¯¯¯=(2+3i)(2−3i)=22−(3i)2=22+32=13
Tổng quát:
Cho số phức z=a+bi. Ta có:
z+z¯=(a+bi)+(a−bi)=2a
z.z¯=(a+bi)(a−bi)=a2−(bi)2=a2+b2=|z|2
* Tổng của một số phức với số phức liên hợp của nó bằng hai lần phần thực của số phức đó.
* Tích của một số phức với số phức liên hợp của nó bằng bình phương môđun bình phương của số phức đó.
Ví dụ 2: Cho z=−3+5i tính z+z¯ and z.z¯
Hướng dẫn giải:
Ta có:
+ z+z¯=2a=−6.
+ z.z¯=a2+b2=34.
2. Phép chia số phức
Ví dụ 3: Tìm số phức z thỏa mãn: (1+i)z=4+2i (1)
Định nghĩa: Chia số số phức c+di cho số phức a+b khác 0 là tìm số phức z sao cho (a+bi)z=c+di. Gọi số phức z gọi là thương của phép chia c+di cho a+b.
Cách tính:
Theo định nghĩa phép chia số phức ta có: (a+bi)z=c+di (1)
Nhân cả hai với số phức liên hợp của a+b ta được:
(a+bi)(a−bi)z = (c+di)(a−bi)⇔(a2+b2)z = ac+bd+(ad−cb)i
Nếu sau khi học xong phần lý thuyết phía trên mà các bạn vẫn chưa hình dung ra cách làm bài thì đừng vội bỏ cuộc nhé, các bạn có thể tham khảo thêm bài giảng của thầy giáo đến từ trung tâm Toppy qua đoạn video dưới đây để hiểu bài học hơn nhé!
Bài tập sách giáo khoa Phép chia số phức
Bài tập sách giáo khoa rất sát với lý thuyết, các bạn hãy cùng itoan chinh phục các bài tập khó nhằn này nhé!
Trả lời câu hỏi Toán 12 Giải tích Bài 3 trang 136:
Cho z = 2 + 3i. Hãy tính z + u– và z.u–. Nêu nhận xét.
Hướng dẫn giải:
u– = 2 – 3i
z + u– = 2 + 3i + 2 – 3i = 4
z . u– = (2 + 3i).(2 – 3i) = 4 – 3i.3i = 4 + 9 = 13.
Ta có: z + u– = Rez và z . u– = |z|2.
Bài 1 (trang 138 SGK Giải tích 12):
Thực hiện các phép chia sau:
Hướng dẫn giải:
Bài 2 (trang 138 SGK Giải tích 12):
Tìm nghịch đảo của z là:
a) z = 1 + 2i
b) z = √2 – 3i
c) z = i
d) z = 5 + i√3
Hướng dẫn giải:
Bài 3 (trang 138 SGK Giải tích 12):
Thực hiện các phép tính sau:
Hướng dẫn giải:
a) 2i(3 + i)(2 + 4i)
= (6i + 2i2)(2 + 4i)
= (-2 + 6i)(2 + 4i)
= (-2.2 – 6.4) + (6.2 – 2.4).i
= -28 + 4i.
b) Ta có:
(1 + i)2.(2i)3 = (1 + 2i + i2).8i.i2
= (1 + 2i – 1).8i .(-1) = -16i2 = 16.
Do đó:
c) 3 + 2i + (6 + i)(5 + i)
= 3 + 2i + (6.5 – 1) + (5 + 6).i
= 3 + 2i + 29 + 11i
= 31 + 13i.
Bài 4 (trang 138 SGK Giải tích 12):
Giải các phương trình sau:
Hướng dẫn giải:
a) (3 – 2i)z + (4 + 5i) = 7 + 3i
⇔ (3 – 2i).z = (7 + 3i) – (4 + 5i)
⇔ (3 – 2i).z = 3 – 2i
⇔ z = 1.
b) (1 + 3i)z – (2 + 5i) = (2 + i)z
⇔ (1 + 3i).z – (2 + i).z = 2 + 5i
⇔ [(1 + 3i) – (2 + i)].z = 2 + 5i
⇔ (-1 + 2i).z = 2 + 5i
Lời kết:
Đến giờ phút này thì bài học Phép chia số phức đã chính thức khép lại, còn bạn nào có điều gì băn khoăn không nhỉ? Mỗi ngày chúng ta dành một chút thời gian đến các bài học Toán thú vị của cô sẽ giúp các bạn nâng cao kiến thức và rèn luyện tư duy tốt hơn. Ngoài ra nếu có thời gian rảnh rỗi, các bạn hãy vào trang website của Toppy, tại đây có thêm các bài tập nâng cao cho các bạn học sinh phấn đấu học lực khá giỏi. Còn bây giờ thì cô và các bạn sẽ chia tay nhau tại đây nhé! Tạm biệt!
Xem thêm bài giảng: