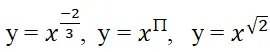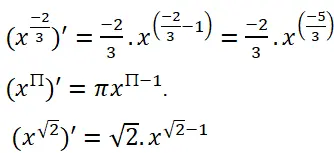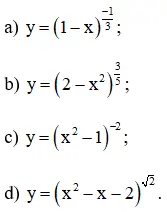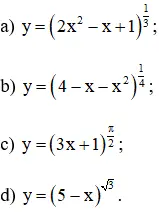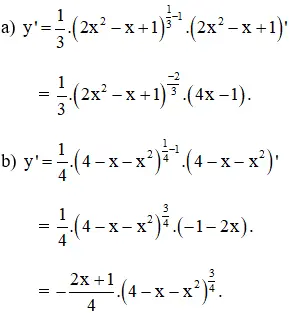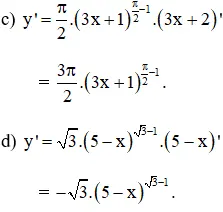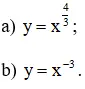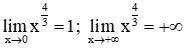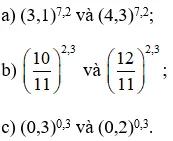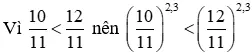Hàm số lũy thừa – Học tốt giải tích 12 cùng itoan

Chào mừng các bạn đã quay trở lại với itoan! Bài học hôm nay là bài Hàm số lũy thừa giúp các em nắm được các yếu tố liên quan đến hàm số lũy thừa như khái niệm, tập xác định, tính đơn điệu, cách tính đạo hàm, các dạng đồ thị của hàm số lũy thừa qua đó sẽ tạo cho các em một nền tảng kiến thức phục vụ cho việc giải bài tập liên quan đến hàm số lũy thừa. Cùng cô học bài hôm nay ngay nhé!
Mục tiêu bài học hàm số lũy thừa
Sau khi học xong bài học này, các em cần nắm được các kiến thức về:
- Nắm vững khái niệm và tập xác định của hàm số lũy thừa,đạo hàm và đồ thị của hàm số lũy thừa.
- Tìm được tập xác định của hàm số lũy thừa,tính được đạo hàm và đồ thị của hàm số lũy thừa, rèn luyện kĩ năng tính toán.
Kiến thức cần nắm hàm số lũy thừa
Bài học hôm nay có một số kiến thức trọng tâm như sau:
1. Định nghĩa: Hàm số y = xα với α ∈ R được gọi là hàm số lũy thừa.
2. Tập xác định: Tập xác định của hàm số y = xα là:
• D = R nếu α là số nguyên dương.
• D = R \ {0} với α nguyên âm hoặc bằng 0
• D = (0; +∝) với α không nguyên.
3. Đạo hàm: Hàm số y = xα có đạo hàm với mọi x > 0 và (xα)’ = α.xα – 1.
4. Tính chất của hàm số lũy thừa trên khoảng (0; +∝).
| y = xα, α > 0 | y = xα, α < 0 |
| a. Tập khảo sát: (0; +∝) | a. Tập khảo sát: (0; +∝) |
| b. Sự biến thiên
+ y’ = αxα – 1 > 0, ∀x > 0
+ Tiệm cận: không có |
b. Sự biến thiên
+ y’ = αxα – 1 < 0, ∀x > 0
+ Tiệm cận: không có – Trục 0x là tiệm cận ngang – Trục 0y là tiệm cận đứng. |
c. Bảng biến thiên 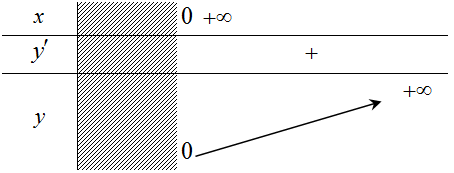 |
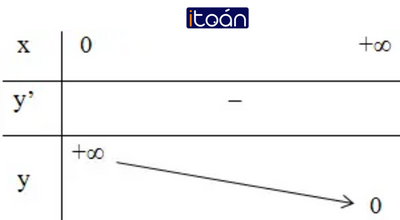
c. Bảng biến thiên 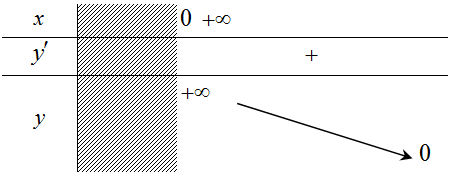 |
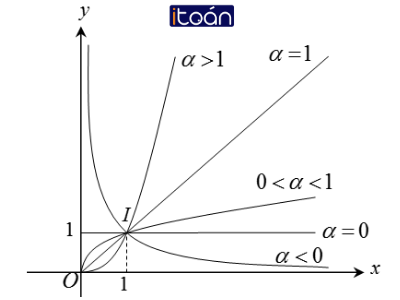
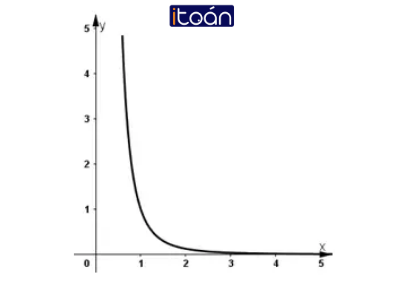
d. Đồ thị:
Đồ thị của hàm số lũy thừa y = xα luôn đi qua điểm I(1; 1)
Lưu ý: Khi khảo sát hàm số lũy thừa với số mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập xác định của nó. Chẳng hạn: y = x3, y = x-2, y = xπ
Hướng dẫn giải bài tập SGK: hàm số lũy thừa
Để nắm chắc lý thuyết, cô và các bạn cùng nhau giải các bài tập trong sách giáo khoa nhé!
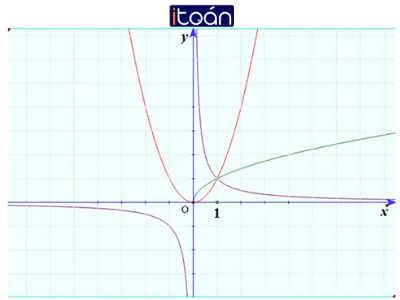
Trả lời câu hỏi Toán 12 Giải tích Bài 2 trang 57: Vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số sau và nêu nhận xét về tập xác định của chúng: y = x^2, y = x^(1/2), y = x^(-1).
Lời giải:
Đồ thị của hàm số y = x2: đường màu đỏ.
Đồ thị của hàm số y = x(1/2): đường màu xanh.
Đồ thị của hàm số y = x(-1) đường màu tím.
Ta có:
Tập xác định của hàm số y = x2 là R.
Tập xác định của hàm số y = x(1/2) là [0,+∞).
Tập xác định của hàm số y = x(-1)là R\{0}.
Trả lời câu hỏi Toán 12 Giải tích Bài 2 trang 57:
Tính đạo hàm của các hàm số:
Lời giải:
y’= [(3x2 – 1)(-√2)]’
= -√2.(3x2 – 1)(-√2-1).(3x2 – 1)’
= -√2.(3x2 – 1)(-√2-1).6x
= -6√2 x.(3x2 – 1)(-√2-1).
Bài 1 (trang 60 SGK Giải tích 12):
Tìm tập xác định của các hàm số:
Lời giải:
a) Hàm số 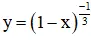
⇔ 1 – x > 0
⇔ x < 1.
Vậy tập xác định D = (-∞; 1).
b) Hàm số xác định
⇔ 2 – x2 > 0
⇔ x2 < 2
⇔ -√2 < x < √2.
Vậy tập xác định D = (-√2; √2).
c) Hàm số
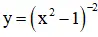
⇔ x2 – 1 > 0
⇔ x2 > 1
⇔ x > 1 hoặc x < -1.
Vậy tập xác định D = (-∞; -1) ∪ (1; +∞).
d) Hàm số xác định
⇔ x2 – x – 2 > 0
⇔ (x + 1)(x – 2) > 0
⇔ x < -1 hoặc x > 2
Vậy tập xác định D = (-∞; -1) ∪ (2; +∞).
Bài 2 (trang 61 SGK Giải tích 12):
Tính đạo hàm của các hàm số:
Lời giải:
Bài 3 (trang 61 SGK Giải tích 12):
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số:
Lời giải:
a) Xét hàm số
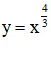
– Tập khảo sát : (0 ; +∞).
– Sự biến thiên:
+ 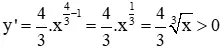
+ Giới hạn:
+ Tiệm cận : Đồ thị hàm số không có tiệm cận.
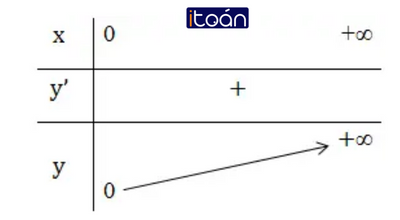
+ Bảng biến thiên:
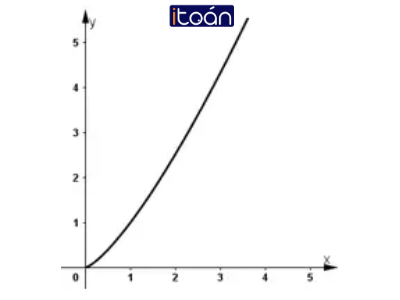
– Đồ thị hàm số:
b) Xét hàm số y = x-3, ta có :
– Tập khảo sát : (0 ; +∞).
– Sự biến thiên:
+ y’ = -3.x-3 – 1 = -3.x-4 < 0 với ∀ x > 0.
+ Giới hạn:
⇒ x = 0 (trục Oy) là tiệm cận đứng của đồ thị hàm số
y = 0 (trục Ox) là tiệm cận ngang của đồ thị hàm số.
+ Bảng biến thiên:
– Đồ thị:
Bài 4 (trang 61 SGK Giải tích 12):
Hãy so sánh các số sau với 1:
a) (4,1)2,7;
b) (0,2)0,3;
c) (0,7)3,2;
d) (√3)0,4
Lời giải:
a) Ta có: 2,7 > 0 nên hàm y = x2,7 luôn đồng biến trên (0 ; +∞).
Vì 4,1 > 1 ⇒ (4,1)2,7 > 12,7 = 1.
b) Ta có : 0,3 > 0 nên hàm số y = x0,3 đồng biến trên (0 ; +∞).
Vì 0,2 < 1 ⇒ 0,20,3 < 10,3 = 1.
c) Ta có: 3,2 > 0 nên hàm số y = x3,2 đồng biến trên (0 ; +∞)
Vì 0,7 < 1 ⇒ 0,73,2 < 13,2 = 1.
d) Ta có: 0,4 > 0 nên hàm số y = x0,4 đồng biến trên (0 ; +∞)
Vì √3 > 1 ⇒ (√3)0,4 > 10,4 = 1.
Bài 5 (trang 61 SGK Giải tích 12):
So sánh
Lời giải:
Hàm số y = xα luôn đồng biến trên (0 ; +∞) với α > 0
a) Ta có : 7,2 > 0
Vì 3,1 < 4,3 nên (3,1)7,2 < (4,3)7,2.
b) Ta có : 2,3 > 0
c) Ta có : 0,3 > 0
Vì 0,3 > 0,2 nên (0,3)0,3 > (0,2)0,3.
Lời kết:
Vậy là chúng ta đã hoàn thành xong bài học Hàm số lũy thừa, các bạn đã nắm được hết nội dung bài học chưa và còn bạn nào có điều gì thắc mắc có thể trao đổi với đội ngũ giáo viên của itoan dưới phần bình luận nhé!. Các bạn có thể xem thêm các bài học hay khác tại Toppy. Toppy sẽ giúp các em làm chủ môn Toán và tìm được niềm yêu thích với môn này! Chúc các bạn đạt được mục tiêu của mình.
Xem thêm các bài viết có liên quan:
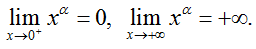 + Giới hạn đặc biệt
+ Giới hạn đặc biệt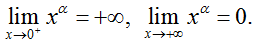 + Giới hạn đặc biệt
+ Giới hạn đặc biệt