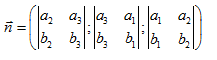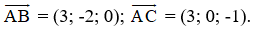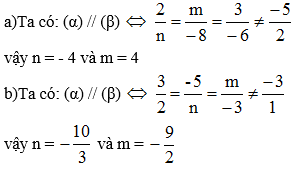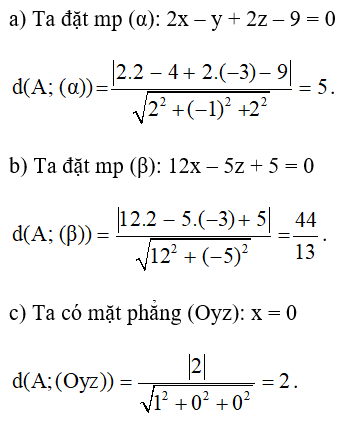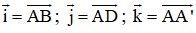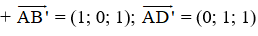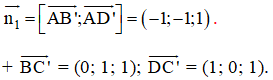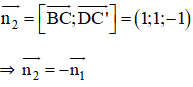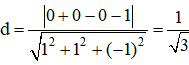Phương trình mặt phẳng – Bài tập & Lời giải Toán 12

Một mặt phẳng trong không gian ba chiều sẽ được xác định như thế nào? Mối tương quan giữa các mặt phẳng với nhau và mặt phẳng với điểm, đường thẳng ra sao? Chúng ta cùng tìm hiểu trong bài học hôm nay: Phương trình mặt phẳng – Bài tập & Lời giải Toán 12 do iToan biên soạn nhé!
Bài giảng gồm 3 phần chính
- Tổng hơp lý thuyết
- Hướng dẫn giải bài tập SGK Hình học 12
- Bài tập tự luyện
Lý thuyết về Phương trình mặt phẳng
Vecto pháp tuyến của mặt phẳng
Cho mp (P).
Nếu vectơ n→≠0→ và có giá vuông góc với (P) thì n→ được gọi là vectơ pháp tuyến của (P).
Chú ý: Nếu n→ là vectơ pháp tuyến của một mặt phẳng thì kn→ với k≠0, cũng là vectơ pháp tuyến của mặt phẳng đó.
Trong KG, cho mp (P) và hai vectơ không cùng phương a→=(a1;a2;a3), b→=(b1;b2;b3) có giá song song hoặc nằm trong (P). Khi đó, nếu n→ là vectơ pháp tuyến của mặt phẳng (P) thì
Vectơ n→ xác định như trên chính là tích có hướng (hay tích vectơ) của hai vectơ a→ và b→ .
Kí hiệu: n→=[a→,b→] hoặc n→=a→∧b→ .
Ví dụ: Tìm một vectơ pháp tuyến của mặt phẳng (P) đi qua 3 điểm A(2;–1;3),B(4;0;1),C(–10;5;3).
Giải
Ta có
AB−→−=(2;1;−2), AC−→−=(−12;6;0).
n→=[AB−→−,AC−→−]=(12;24;24) là một vectơ pháp tuyến của mặt phẳng (P).
Phương trình tổng quát của mặt phẳng
1. Định nghĩa:
Phương trình Ax+By+Cz+D=0, trong đó A2+B2+C2≠0, được gọi là phương trình tổng quát của mặt phẳng.
Nhận xét:
a) (P): Ax+By+Cz+D=0 ⇒ (P) có 1 VTPT là n→=(A;B;C).
b) PT của (P) qua M0=(x0;y0;z0) và có VTPT n→=(A;B;C) là: A(x−x0)+B(y−y0)+C(z−z0)=0
Ví dụ 1: Cho mặt phẳng (P) có phương trình 2x+3y−z+2=0. Tìm một véctơ pháp tuyến của mặt phẳng.
Giải
Một véctơ pháp tuyến của (P) là n→=(2;3;−1) .
Ví dụ 2: Viết phương trình mặt phẳng đi qua điểm M0=(1;−2;3) và có vectơ pháp tuyến n→=(−2;1;4) .
Giải
Phương trình mặt phẳng (P) qua M0=(1;−2;3) và có VTPT n→=(−2;1;4) là:
−2(x−1)+1(y+2)+4(z−4)=0 ⇔ −2x+y+4z−12=0
2. Các trường hợp riêng
Trong không gian Oxyz, cho mặt phẳng (P):
Ax+By+Cz+D=0 (1)
Nếu D=0 thì (P) đi qua gốc tọa độ O.
Nếu A=0 thì [(P)⊂Ox(P)//Ox().
Nếu A=B=0 ⇔ [(P)//(0xy)(P)≡(Oxy)()
Khi đó mặt phẳng (P) cắt các trục Ox,Oy,Oz lần lượt tại A(a;0;0),B(0;b;0),C(0;0;c) . Phương trình (2) được gọi là phương trình của mặt phẳng theo đoạn chắn.
Ví dụ: Trong không gian Oxyz, cho ba điểm M(1;0;0),N(0;2;0),P(0;0;3). Hãy viết phương trình mặt phẳng (MNP).
Giải
Áp dụng phương trình mặt phẳng theo đoạn chắn, ta có phương trình mặt phẳng (MNP) là
x/1+y/2+z/3=1
Hay 6x+3y+2z−6=0.
Điều kiện hai mặt phẳng song song, vuông góc
1. Điều kiện hai mặt phẳng song song
Trong không gian Oxyz cho 2 mặt phẳng (P1),(P2) có phương trình
(P1): A1x+B1y+C1z+D1=0
(P2): A2x+B2y+C2z+D2=0
• (P1)//(P2)
• (P1) cắt (P2)
⇔ n1−→≠kn2−→ ⇔ (A1;B1;C1)≠k(A2;B2;C2)
Ví dụ: Viết PT mp (P) đi qua điểm M(1;−2;3) và song song với mp (Q):2x−3y+z+5=0 .
Giải
Vì (P)//(Q) nên (P) có VTPT n→=(2;−3;1) .
⇒ (P):2(x−1)−3(y+2)+1(z−3)=0
⇔ 2x−3y+z−11=0.
2. Điều kiện hai mặt phẳng vuông góc
Trong không gian Oxyz cho 2 mặt phẳng (P1), (P2) có phương trình
(P1): A1x+B1y+C1z+D1=0
(P2): A2x+B2y+C2z+D2=0
(P1) ⊥ (P2) ⇔ n1−→.n2−→=0
⇔ A1A2+B1B2+C1C2=0
Ví dụ:
1) Xác định m để hai mp sau vuông góc với nhau:
(P):2x−7y+mz+2=0
(Q):3x+y−2z+15=0
2) Viết phương trình mp (P) đi qua hai điểm A(3;1;−1,B(2;−1;4) và vuông góc với mp (Q):2x−y+3z−1=0 .
Giải
1) (P) ⊥ (Q) ⇔ A1A2+B1B2+C1C2=0 ⇔ m=−12
2) (P) có cặp vectơ chỉ phương là:
AB−→−=(−1;−2;5) và nQ−→=(2;−1;3).nP−→=[AB−→−,nQ−→]=(−1;13;5) ⇒ (P):x−13y−5z+5=0
Khoảng cách từ một điểm đến một mặt phẳng
Định lí: Trong không gian Oxyz, cho (P):Ax+By+Cz+D=0 và điểm M0(x0;y0;z0). Khoảng cách từ điểm M0 đến mặt phẳng (P), kí hiệu là d(M0,(P)), được tính theo công thức:
Giải bài tập SGK Phương trình mặt phẳng
Bài 1: Viết phương trình mặt phẳng:
a) Đi qua điểm M(1; -2; 4) và nhận n→ = (2 ; 3 ; 5) làm vec tơ pháp tuyến
b) Đi qua A(0; -1; 2) và song song với giá của mỗi vec tơ u→ = (3; 2; 1) và v→ = (-3; 0; 1).
c) Đi qua ba điểm A(-3; 0; 0); B(0; -2; 0) và C(0; 0; -1).
Lời giải:
a) Mặt phẳng đi qua điểm M(1; -2; 4) và nhận n→ = (2; 3; 5) làm vectơ pháp tuyến là:
2(x – 1) + 3(y + 2) + 5(z – 4) = 0
⇔ 2x + 3y + 5z – 16 = 0.
b) Mặt phẳng nhận u→ và v→ là vec tơ chỉ phương
⇒ nhận 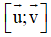
Mặt phẳng đi qua A(0 ; -1 ; 2) nên có phương trình :
2(x – 0) – 6(y + 1) + 6(z – 2) = 0
⇔ 2x – 6y + 6z – 18 = 0
⇔ x – 3y + 3z – 9 = 0
c)
Mặt phẳng (R) đi qua ba điểm A, B, C nhận 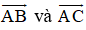
⇒ Nhận 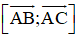
(R) đi qua A(-3; 0; 0) nên có phương trình:
2(x + 3) + 3y + 6z = 0
⇔ 2x + 3y + 6z + 6 = 0.
Bài 2
Viết phương trình mặt phẳng trung trực của đoạn thẳng AB với A(2; 3; 7), B(4; 1; 3)
Lời giải:
Bài 3
a) Lập phương trình của các mặt phẳng tọa độ Oxy, Oyz và Ozx
b) Lập phương trình của các mặt phẳng đi qua điểm M(2; 6; -3) và lần lượt song song với các mặt phẳng tọa độ.
Lời giải:
a) Mặt phẳng Oxy là tập hợp các điểm có cao độ z = 0 nên có phương trình: z = 0.
Tương tự:
Mặt phẳng Oyz: x = 0
Mặt phẳng Ozx: y = 0.
b) Phương trình mặt phẳng đi qua M(2; 6; -3) và song song với (Oxy): z + 3 = 0
Phương trình mặt phẳng đi qua M(2; 6; -3) và song song với (Oyz): x – 2 = 0
Phương trình mặt phẳng đi qua M(2; 6; -3) và song song với (Ozx): y – 6 = 0.
Bài 4: Lập phương trình mặt phẳng:
a)Chứa trục Ox và điểm P(4; -1; 2)
b)Chứa trục Oy và điểm Q(1; 4; -3)
c)Chứa trục Oz và điểm R(3; -4; 7)
Lời giải:
a) (P) chứa Ox và điểm P(4; -1; 2).
+ (P) chứa Ox ⇒ nhận i→ = (1; 0; 0) là 1 vtcp
+ (P) chứa O(0 ; 0 ; 0) và P(4 ; -1 ; 2) ⇒ nhận 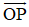
⇒ (P) nhận 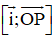
⇒ (P): -2.(y – 0) – 1.(z – 0) = 0
hay (P) : 2y + z = 0.
b) (Q) chứa trục Oy và điểm Q(1; 4; -3)
+ (Q) chứa Oy ⇒ nhận j→ = (0; 1; 0) là 1 vtcp).
+ (Q) chứa O(0 ; 0 ; 0) và Q(1 ; 4 ; -3) ⇒ nhận 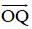
⇒ (Q) nhận 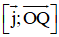
⇒ (Q): -3(x – 0) – 1.(z – 0) = 0
hay (Q): 3x + z = 0.
c) (R) chứa trục Oz và điểm R(3; -4; 7)
+ (R) chứa Oz ⇒ nhận k→ = (0; 0; 1) là 1 vtcp.
+ (R) chứa O(0 ; 0 ; 0) và R(3 ; -4 ; 7) ⇒ nhận 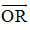
⇒ (R) nhận 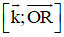
⇒ (R): 4(x – 0) + 3.(y – 0) = 0
hay (R): 4x + 3y = 0.
Bài 5
Cho tứ diện có các đỉnh là A(5; 1; 3), B(1; 6; 2), C(5; 0; 4), D(4; 0; 6)
a)Hãy viết phương trình của các mặt phẳng (ACD) và (BCD)
b)Hãy viết phương trình mặt phẳng (α) đi qua cạnh AB và song song với cạnh CD.
Lời giải:
Bài 6
Hãy viết phương trình mặt phẳng (α) đi qua điểm M(2; -1; 2) và song song với mặt phẳng (β) : 2x – y + 3z + 4 = 0
Lời giải:
Vì mặt phẳng (α) song song với mặt phẳng ( β) : 2x – y + 3z + 4 = 0 nên phương trình của mp(α) có dạng 2x – y + 3z + D = 0
Vì M(2; -1; 2) ∈ mp(α) nên 4 + 1 + 6 + D = 0 <=> D = -11
Vậy phương trình của mp(α) là: 2x – y + 3z – 11= 0
Bài 7
Lập phương trình mặt phẳng (α) qua hai điểm A(1; 0; 1), B(5; 2; 3) và vuông góc với mặt phẳng ( β) : 2x – y + z – 7 = 0
Lời giải:
Bài 8
Xác định các giá trị của m và n để mỗi cặp mặt phẳng sau đây là một cặp mặt phẳng song song với nhau;
a)2x + my + 3z – 5 = 0 và nx – 8y – 6z + 2 =0
b)3x – 5y + mz – 3 = 0 và 2x + ny – 3z + 1 = 0
Lời giải:
Bài 9
Tính khoảng cách từ điểm A(2; 4; -3) lần lượt đến các mặt phẳng sau:
a) 2x – y + 2z – 9 = 0 (α)
b) 12x – 5z + 5 = 0 ( β)
c) x = 0 ( γ;)
Lời giải:
Bài 10
giải bài toán sau đây bằng phương pháp tọa độ:
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1.
a)Chứng minh hai mặt phẳng (AB’D’) và (BC’D) song song.
b)Tính khoảng cách giữa hai mặt phẳng nói trên.
Lời giải:
Chọn hệ trục tọa độ Oxyz có gốc O ≡ A;
⇒ A(0; 0; 0) ; B(1; 0; 0); C(1; 1; 0); D(0; 1; 0).
A’(0; 0; 1); B’(1; 0; 1); C’(1; 1; 1); D’(0; 1; 1).
a)
⇒ Vectơ pháp tuyến của (AB’D’) là:
⇒ Vectơ pháp tuyến của (BC’D) là:
⇒ (AB’D’) // (BC’D).
b) Mặt phẳng (BC’D) có VTPT 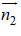
1( x- 1) + 1( y – 0) – 1( z- 0)= 0 hay x + y – z – 1 = 0
Khoảng cách giữa hai mặt phẳng song song (AB’D’) và (BC’D) chính là khoảng cách từ A đến (BC’D) và bằng :
Lời kết:
Để học tốt chương trình Toán hình học 12 và ôn tập thật kĩ cho các kì thi sắp tới, các em cần đọc lại phần lý thuyết, thành thạo các bài tập sách giáo khoa và tích cực ôn tập các bài tập trắc nghiệm tự luyện. Các bài tập tự luyện đa dạng từ cơ bản đến nâng cao theo từng chủ đề đều có tất cả trên website Toppy. Toppy sẽ giúp các em tiến bộ và nâng cao kiến thức.
>> Xem thêm:
- Tính chất của hai tiếp tuyến cắt nhau
- Phương trình đường thẳng
- Phương trình lượng giác cơ bản
- Đường thẳng và mặt phẳng