Số phần tử của một tập hợp, tập hợp con – Hướng dẫn giải bài tập Toán 6

Bài học: Số phần tử của một tập hợp, tập hợp con là một bài học quan trọng trong chương trình học Đại số lớp 6. Bài giảng được cô biên soạn có nội dung trọng tâm bài học đơn giản, dễ hiểu và được đan xen những hình ảnh sinh động giúp các em không bị nhàm chán trong quá trình học. Đặc biệt là bài giảng còn có đáp án chi tiết các bài tập giúp các em theo dõi bài tốt hơn. Cùng đến với bài học của cô nhé!
Mục tiêu bài học Số phần tử của một tập hợp, tập hợp con
Trước mỗi bài học, chúng ta đều đặt ra cho mình những mục tiêu nhất định để tạo động lực học bài!
- Hiểu khái niệm và cách đọc của tập hợp.
- Các bài tập liên quan đến liệt kê các phần tử.
- Khái niệm về Tập hợp con.
- Cách làm bài tập liên quan đến Số phần tử của một tập hợp, tập hợp con.
Kiến thức Số phần tử của một tập hợp, tập hợp con
Lý thuyết của bài học hôm nay khá dễ hiểu, các bạn chú ý ghi chép lại bài học nhé!
1. Số phần tử của một tập hợp
Ví dụ:
Các tập hợp sau có bao nhiêu phần tử? Đáp án:
H ={ 1 } 1 phần tử
L = {bóng đá, bóng rổ, bóng chuyền} 3 phần tử
M = { x∈N| 1<x } Vô số phần tử
N = { x∈N| x2+1=0 } Không có phần tử nào
Kết luận:
Một tập hợp có thể có một phần tử, nhiều phần tử, vô số phần tử hoặc không có phần tử nào.
Tập hợp không có phần tử nào gọi là tập hợp rỗng, kí hiệu là ∅.
2. Tập hợp con
Ví dụ: Cho 2 tập hợp:
A = {các học sinh lớp 6A}
G = {các học sinh nữ lớp 6A}
Hiển nhiên, các học sinh nữ lớp 6A đều nằm trong số các học sinh lớp 6A, ta nói tập G là tập con của tập A.
Kết luận: Nếu mọi phần tử của tập hợp A đều thuộc tập hợp B thì tập hợp A gọi là tập hợp con của tập hợp B.
Kí hiệu:A⊂B hoặc B⊂A.
Lưu ý: Nếu A⊂B và B⊂A, thì A và B là hai tập hợp bằng nhau, kí hiệu A=B.
Nếu học qua phần lý thuyết rồi mà vẫn còn nhiều khó khăn, các em có thể xem bài giảng của cô giáo Yên Bình xinh đẹp đến từ Toppy dưới đây nhé!
Giải bài tập SGK Số phần tử của một tập hợp, tập hợp con
Phần bài tập trong sách giáo khoa rất sát với lý thuyết chúng ta cần nhớ. Vậy nên các bạn chú ý giải hết rồi kiểm tra với đáp án của cô nhé!
Bài 16. (SGK Toán 6 Trang 13 )
Mỗi tập hợp sau có bao nhiêu phần tử ?
a) Tập hợp các số tự nhiên
mà
.
b) Tập hợp các số tự nhiên
mà
.
c) Tập hợp các số tự nhiên
mà
.
d) Tập hợp các số tự nhiên
mà
.
Hướng dẫn giải:
a) . Tập
có
phần tử.
b) . Tập
có
phần tử.
c) . Tập
có vô số phần tử.
d) . Tập
không có phần tử nào.
Bài 17. (SGK Toán 6 Trang 13 )
Viết các tập hợp sau và cho biết mỗi tập hợp có bao nhiêu phần tử ?
a) Tập hợp các số tự nhiên không vượt quá
.
b) Tập hợp các số tự nhiên lớn hơn
nhưng nhỏ hơn
.
Hướng dẫn giải:
a) . Tập hợp
có
phần tử.
b) . Tập hợp
không có phần tử nào (vì giữa hai số tự nhiên
và
không có số tự nhiên nào khác).
Bài 18. (SGK Toán 6 Trang 13 )
Cho . Có thể nói rằng
là tập hợp rỗng hay không ?
Hướng dẫn giải:
Với ta nói rằng tập hợp
có một phần tử, đó là phần tử
. Do đó nói
là không đúng.
Bài 19. (SGK Toán 6 Trang 13 )
Viết các tập hợp các số tự nhiên nhỏ hơn , tập hợp các số tự nhiên nhỏ hơn , rồi dùng kí hiệu để thể hiện quan hệ giữa hai tập hợp trên.
Hướng dẫn giải:
Ta thấy mọi phần tử của tập hợp đều là phần tử của tập hợp
.
Vậy .
Bài 20. (SGK Toán 6 Trang 13 )
Cho tập hợp . Điền kí hiệu
hoặc
vào chỗ trống cho đúng:
a)
b)
c)
Hướng dẫn giải:
Nhận xét: Tập hợp A={15,24} là tập hợp có hai phần tử là 15 và 24.
Câu a: Vì 15 là một phần tử của A nên ta viết 15 ∈ A.
Câu b: Vì 15 ∈ A nên {15} ⊂ A.
Câu c: {15; 24} = A.
Bài 21. (SGK Toán 6 Trang 13 )
Tập hợp có
(phần tử).
Tổng quát: Tập hợp các số tự nhiên từ đến
có
phần tử.
Hãy tính số phần tử của tập hợp sau: .
Hướng dẫn giải:
Tập hợp có
phần tử.
Bài 22. (SGK Toán 6 Trang 13 )
Hướng dẫn giải:
a) C = {0; 2; 4; 6; 8}
b) L = {11; 13; 15; 17; 19}
c) A = {18; 20; 22}
d) B = {25; 27; 29; 31}.
Bài 23. (SGK Toán 6 Trang 13 )
Tập có
(phần tử).
Tổng quát:
– Tập hợp các số chẵn từ số chẵn đến số chẵn
có
phần tử.
– Tập hợp các số lẻ từ số lẻ đến số lẻ
có
phần tử.
Hãy tính số phần tử của các tập hợp sau:
Hướng dẫn giải:
Tập hợp có
phần tử.
Tập hợp có
phần tử.
Bài 24. (SGK Toán 6 Trang 13 )
Cho:
là tập hợp các số tự nhiên nhỏ hơn
,
là tập hợp các số chẵn,
là tập hợp các số tự nhiên khác
.
Dùng kí hiệu để thể hiện quan hệ của mỗi tập hợp trên với tập hợp
các số tự nhiên.
Hướng dẫn giải:
Tập hợp
Tập hợp
Tập hợp
Tập hợp các số tự nhiên
Nhận thấy mọi phần tử của tập hợp đều thuộc tập hợp .
Do đó:
Bài 25. (SGK Toán 6 Trang 13 )
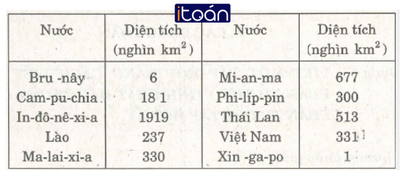
Cho bảng sau (theo Niên giám năm 1999)
Hướng dẫn giải:
Sắp xếp các diện tích theo thứ tự từ lớn đến nhỏ là
1919>677>513>331>330
Do vậy các nước có diện tích nhỏ dần theo thứ tự là:
In-đô-nê-xi-a; Mi-an-ma; Thái Lan; Việt Nam; Ma-lai-xi-a; Phi-líp-pin; Lào; Cam-pu-chia; Bru-nây; Xin-ga-po.
Vậy
A = {In-đô-nê-xi-a; Mi-an-ma; Thái Lan; Việt Nam}.
B = {Xin-ga-po; Bru-nây; Cam-pu-chia}.
Bài tập tự luyện Số phần tử của một tập hợp, tập hợp con
Phần bài tập tự luyện này cô biên soạn dành riêng cho các bạn, cùng nhau đi tìm lời giải thôi nào!
Bài tập 1: Tập hợp A={x∈N|x.1=6} được viết dưới dạng liệt kê các phần tử là:
A. A={5}
B. A={6}
C. A
D. A={5;6}
Bài tập 2: Cho các tập hợp X={2;4;5;7;9;10} và Y={1;4;7;5;9}. Chọn khẳng định đúng:
A. Có 5 phần tử thuộc cả hai tập hợp.
B. Có 4 phần tử cùng thuộc cả hai tập hợp.
C. Tập hợp Y là tập con của tập hợp X .
D. Số tập con gồm 2 phần tử của X là 3 .
Bài tập 3: Liệt kê các phần tử của tập hợp A={x∈N|17<x≤27} ta được:
A. A={18;19;20;21;22;23;24;25;26;27}
B. A={17;18;19;20;21;22;23;24;25;26;27}
C. A={18;19;20;21;22;23;24;25;26}
D. A
Hướng dẫn giải bài tập
Bài tập 1: B
Bài tập 2: B
Bài tập 3: A
Lời kết:
Vậy là bài học Số phần tử của một tập hợp, tập hợp con đã khép lại tậ đây. Chúc mừng các em đã đạt được mục tiêu đề ra trong bài học. Để luyện tập nhiều hơn, các bạn hãy đến với Toppy . Ở đó có đầy đủ bài tập từ cơ bản đến nâng cao, giúp các bạn nắm vững bài học. Tạm biệt các em!
Xem thêm: