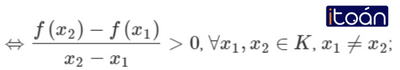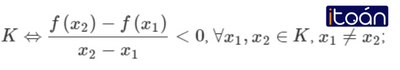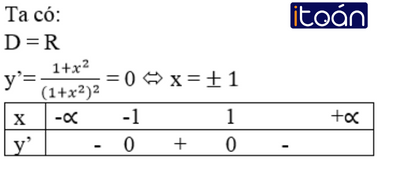Sự đồng biến nghịch biến của hàm số- Học tốt Giải Tích 12

Chào mừng các bạn đã đến với bài học mới của itoan hôm nay. Bài giảng: Sự đồng biến nghịch biến của hàm số – GIải tích 12 được itoan biên soạn theo chương trình sách giáo khoa của Bộ giáo dục. Hy vọng bài giảng này sẽ giúp các em vượt qua các khó khăn, bỡ ngỡ khi học môn Giải tích lớp 12. Mời các em học sinh thân yêu tham khảo!
Mục tiêu bài học Sự đồng biến nghịch biến của hàm số
- Biết hàm số đơn điệu là gì.
- Biết mối liên hệ giữa tính đồng biến, nghịch biến của một hàm số và dấu của đạo hàm cấp một của nó.
- Biết cách xét tính đồng biến, nghịch biến của một hàm số trên một khoảng dựa vào dấu đạo hàm cấp một.
Kiến thức cơ bản của bài học Sự đồng biến nghịch biến của hàm số
Sau đây , chúng ta cùng nhau đi học những kiến thức cơ bản nhất của bài học hôm nay , các bạn hãy tập trung để hiểu bài ngay nhé!
I. Nhắc lại tính đơn điệu của hàm số
Giả sử hàm số y=f(x) xác định trên K (K là khoảng hoặc đoạn hoặc nửa khoảng). Khi đó:
- Hàm số f(x) đồng biến (tăng) trên K nếu với mọi cặp x1 , x2 ∈ K mà x1<x2 thì f(x1)<f(x2) ;
- Hàm số f(x) nghịch biến (giảm) trên K nếu với mọi cặp x1 , x2 ∈ K mà x1<x2 thì f(x1)>f(x2) .
- Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là hàm số đơn điệu trên K.
Nhận xét:
- f(x) đồng biến trên K
- f(x) nghịch biến trên K
- Nếu hàm số đồng biến trên K thì đồ thị đi lên từ trái sang phải.
- Nếu hàm số nghịch biến trên K thì đồ thị đi xuống từ trái sang phải.
Định lí:
Cho hàm số f(x) có đạo hàm trên K:
- Nếu f′(x)>0 với mọi x ∈ K thì hàm số f(x) đồng biến trên K .
- Nếu f′(x)<0 với mọi x ∈ K thì hàm số f(x) nghịch biến trên K .
Chú ý: Nếu f′(x)=0 với mọi x ∈ K thì hàm số f(x) không đổi trên K .
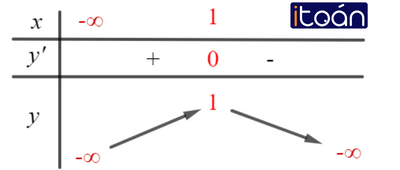
Ví dụ 1: Tìm các khoảng đơn điệu của hàm số: y=−x2+2x
Giải
Tập xác định của hàm số: D=R
Ta có: y′=−2x+2 ; y′=0 ⇔x=1
Bảng biến thiên:
Vậy hàm số đồng biến trên khoảng (−∞ ; 1) và nghịch biến trên khoảng (1,+∞) .
Định lí mở rộng
- Nếu f′(x)≥0 với mọi x∈K và f′(x)=0 chỉ tại một số hữu hạn điểm thuộc K thì f đồng biến trên K.
- Nếu f′(x)≤0 với mọi x∈K và f′(x)=0 chỉ tại một số hữu hạn điểm thuộc K thì f nghịch biến trên K.
Ví dụ 2: Tìm các khoảng đơn điệu của hàm số y=2x3+6x2+6x−7
Giải
Tập xác định của hàm số: D=R
Ta có: y′=6x2+12x+6=6(x+1)2
Do đó y′=0⇔x=−1 và y′>0 với mọi x≠−1.
Theo định lí trên hàm số luôn luôn đồng biến.
II. Quy tắc xét tính đơn điệu của hàm số
Bước 1: Tìm tập xác định. Tính f′(x)
Bước 2: Tìm các điểm mà tại đó f′(x) bằng 0 hoặc f′(x) không xác định.
Bước 3: Sắp xếp các điểm đó theo thứ tự tăng dần và lập bảng biến thiên.
Bước 4: Nếu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Các bạn có thể xem bài giảng chi tiết tại đây!
Hướng dẫn giải bài tập toán SGK Sự đồng biến nghịch biến của hàm số
Để có cái nhìn tổng quan về bài học và kiểm tra kiến thức mà mình nắm được từ đầu đến bây giờ thì chúng ta hãy cùng nhau đi làm một số bài tập SGK
Bài 1 (trang 9 SGK Giải tích 12)
1. Xét sự đồng biến, nghịch biến của hàm số:
Lời giải:
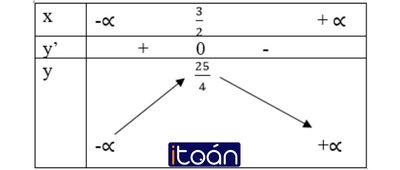
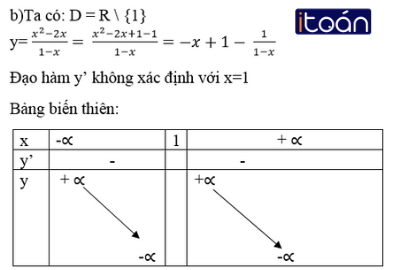
a) Ta có: D = R
y’= 3 – 2x = 0 <=> x = 3/2
Bảng biến thiên:
Trong bảng biến thiên thì hàm số đồng biến trong khoảng ( – ∞; 3/2 ) và nghịch biến trong khoảng ( 3/2 ; + ∞ ).
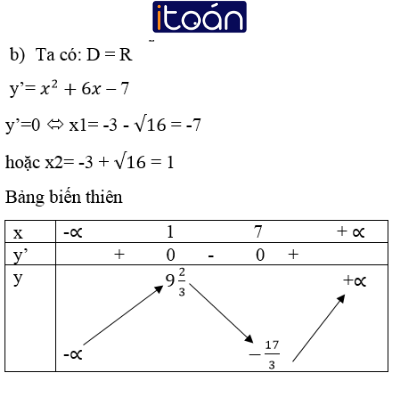
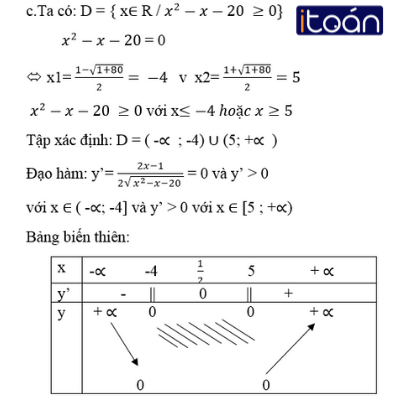
Theo bảng biến thiên, hàm số đồng biến trong các khoảng (-∞ ; 7) và (1 ; +∞ ); nghịch biến trong khoảng ( -7; 1).
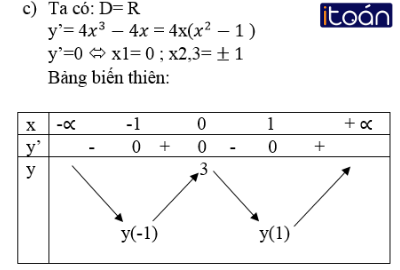
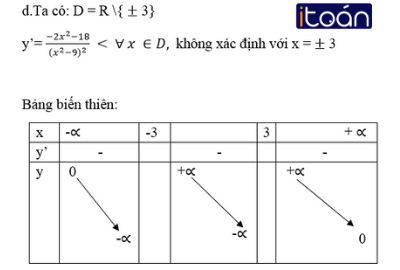
Theo bảng biến thiên thì hàm số nghịch biến trong các khoảng ( -∞ ;1) và (0 ;1); đồng biến trong các khoảng ( -1 ; 0) và ( 1; +∞).
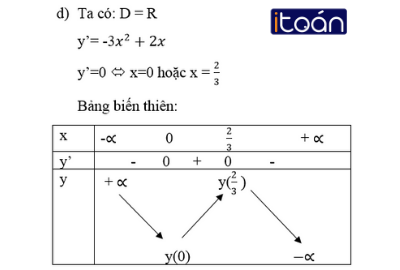
Theo bảng biến thiên thì hàm số nghịch biến trong các khoảng (-∞ ; 0) và (2/3 ; + ∞), đồng biến trong khoảng ( 0 ; 2/3 ).
Bài 2 (trang 10 SGK Giải tích 12):
Lời giải:
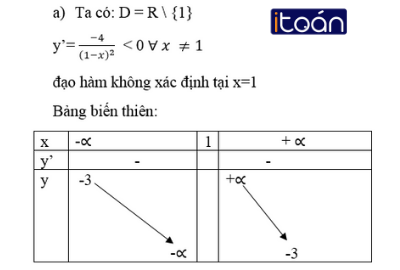
Theo bảng biến thiên thì hàm số nghịch biến trong các khoảng ( -∝ ; 1) và ( 1 ; +∝ ).
Theo bảng biến thiên thì hàm số nghịch biến trong các khoảng (-∝ ;1) và (1 ; +∝)
Theo bảng biến thiên, hàm số nghịch biến trong nửa khoảng (- ∝ ; -4] và đồng biến trong nửa khoảng [ 5 ; + ∝).
Theo bảng biến thiên thì hàm số nghịch biến trong các khoảng đó nên hàm số nghịch biến trong khoảng (-∝ ; -3) ( -3; 3) và ( 3; +∝ )
Bài 3 (trang 10 SGK Giải tích 12):
Lời giải:
Hàm số có đạo hàm trong (-1; 1) và không gian âm khoảng đó nên hàm số đồng biến trong khoảng (-1;1).
Ta có y’< 0 ∀ x ∈ (-∝; -1) ∪ (1; +∝)
Vậy hàm số nghịch biến trong các khoảng (-∝; -1) và (1; +∝).
Bài 4 (trang 10 SGK Giải tích 12):
Chứng minh rằng hàm số y = √(2x-x)2đồng biến trên khoảng ( 0; 1), nghịch biến trên khoảng (1; 2).
Lời giải:
Hàm số có đạo hàm trong tập xác định và y’ > 0 với x ∈ (0; 1) do đó đồng biến trên khoản (0; 1); y’<0 với x ∈ (1; 2) nên nghịch biến trên khoảng (1; 2).
Bài 5 (trang 10 SGK Giải tích 12):
Lời giải:
Một số bài tập luyện cho bài học Sự đồng biến sự nghịch biến
Nhằm giúp các bạn luyện tập thêm tư duy làm bài và củng cố kiến thức bài , chúng ta sẽ cùng nhau làm thêm một số bài tập bổ sung sau đây
Bài tập 1:
Hàm số y=−x3+3x2−4 đồng biến trên tập hợp nào trong các tập hợp được cho dưới:
A. (2;+∞)
B. (0;2)
C. (−∞;0)∪(2;+∞)
D. (−∞;0)
Bài tập 2.
Cho hàm số y=−x3+3x2−1, kết luận nào sau đây về tính đơn điệu của hàm số là đúng:
A. Hàm số đồng biến trên khoảng (0;2) và nghịch biến trên các khoảng (−∞;0); (2;+∞)
B. Hàm số đồng biến trên khoảng (−2;0)
C. Hàm số nghịch biến trên khoảng (0;2) và đồng biến trên các khoảng (−∞;0) ;(2;+∞)
D. Hàm số nghịch biến trên các khoảng (−∞;−2) và (0;+∞)
Bài tập 3.
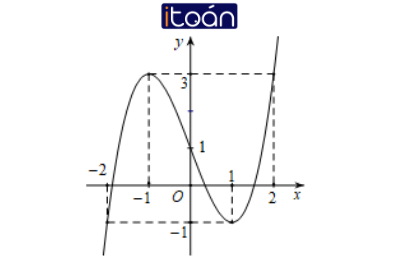
Cho hàm số y=f(x) có đồ thị như hình vẽ. Hàm số đã cho nghịch biến trên khoảng nào?
A. (−1;1)
B. (−2;−1)
C. (−1;2)
D. (1;+∞)
Đáp án bài tập tự luyện
Bài tập 1. B
Bài tập 2. A
Bài tập 3. A
Lời kết
Trên đây là toàn bộ lý thuyết và các dạng bài tập của của bài học này . Itoan mong rằng các bạn đều đã nắm bặt được thật tốt các lý thuyết cũng như cách giải bài tập liên quan đến bài học. Hệ thống bài giảng và phương pháp giải các bài toán chi tiết bài học Sự đồng biến nghịch biến của hàm số sẽ giúp các bạn có phương án học tập và luyện tập bài học tốt nhất . Ngoài ra, các bạn có thể tự tìm hiểu nhiều bài giảng bổ ích khác qua trang Toán của Toppy. Chúc các bạn sẽ thành công trong việc làm chủ môn Giải tích 11 và đạt thật nhiều điểm thưởng.
Xem thêm: