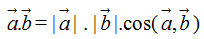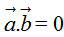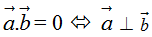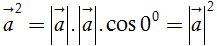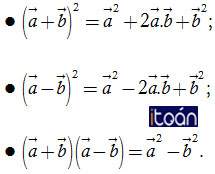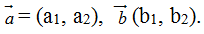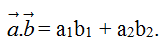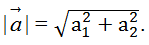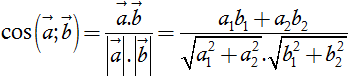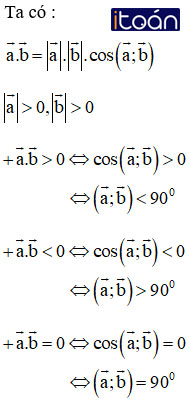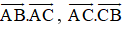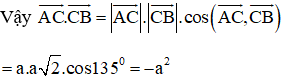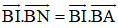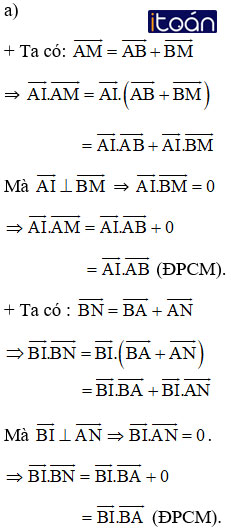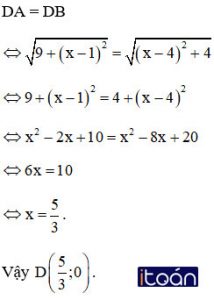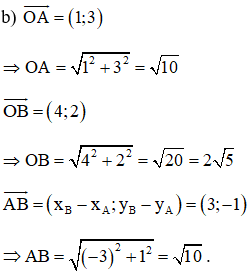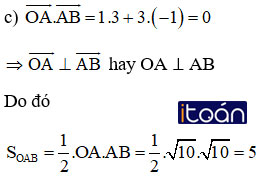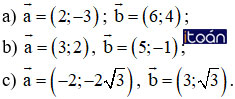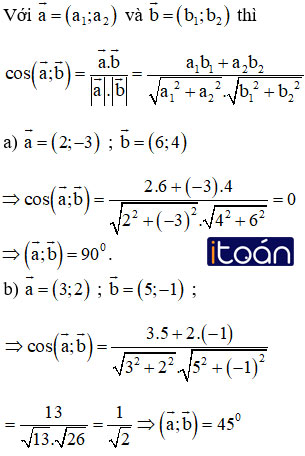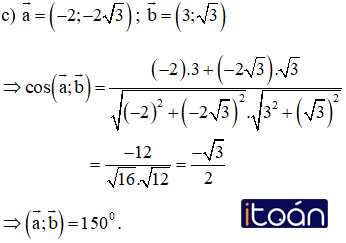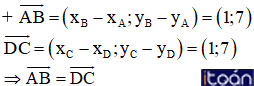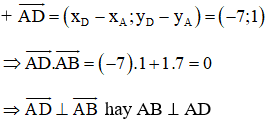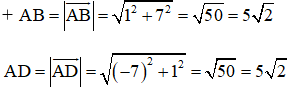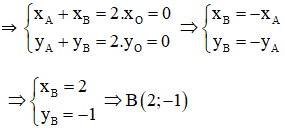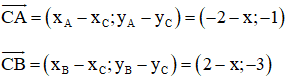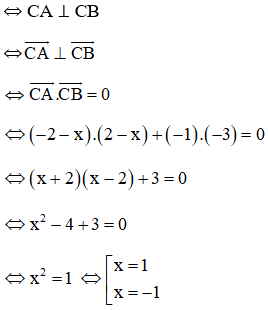Tích vô hướng của 2 vecto – Học toán lớp 10 cùng itoan

Bài học hôm nay, chúng ta sẽ cùng nhau học Tích vô hướng của 2 vecto. Đối với nhiều bạn Tích vô hướng của 2 vecto là phần kiến thức khá phức tạp và khó hiểu của chương trình hình học lớp 10. Tuy nhiên, các em học sinh cũng đừng quá lo lắng và nản chí vì itoan đã tổng hợp tất cả các kiến thức quan trọng của bài học này trong bài viết dưới đây. Cùng iToan theo dõi nhé!
Mục tiêu bài học
Trước khi đi vào bài học chính, các em hãy cùng itoan xác định mục tiêu cần đạt được sau buổi học ngày hôm nay nhé!
- Nắm chắc lý thuyết: Tích vô hướng của 2 vecto là gì?
- Áp dụng kiến thức lý thuyết vào bài tập Tích vô hướng của 2 vecto.
Lý thuyết
1. Định nghĩa
Cho hai vectơ 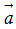
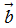
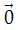
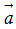
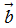
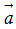
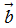
Trường hợp ít nhất một trong hai vectơ 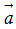
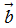
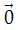
Chú ý
+) Với 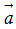
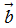
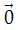
+) Khi 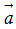
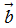
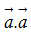
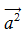
Ta có:
2. Các tính chất của tích vô hướng
Người ta chứng minh được các tính chất sau đây của tích vô hướng:
Nhận xét. Từ các tính chất của tích vô hướng của hai vectơ ta suy ra:
3. Biểu thức tọa độ của tích vô hướng
Trên mặt phẳng tọa độ 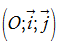
Khi đó tích vô hướng 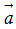
Nhận xét.
Hai vectơ: 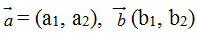
4. Ứng dụng
a) Độ dài của vectơ
Độ dài của vectơ 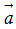
b) Góc giữa hai vectơ
Từ định nghĩa tích vô hướng của hai vectơ ta suy ra nếu 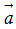
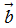
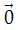
c) Khoảng cách giữa hai điểm
Khoảng cách giữa hai điểm A(xA; yA) và B(xB; yB) được tính theo công thức:
Bài tập sách giáo khoa
Bài 2 trang 42:
Cho hai vectơ a→ và b→đều khác 0→. Khi nào thì tích vô hướng của hai vectơ đó là số dương ? Là số âm ? Bằng 0 ?
Hướng dẫn giải:
Bài 2 trang 44:
Trên mặt phẳng tọa độ Oxy cho ba điểm A(2; 4), B(1; 2), C(6; 2). Chứng minh vectơ AB ⊥ vectơ AC.
Bài 1 (trang 45 SGK Hình học 10):
Cho tam giác vuông cân ABC có AB = AC = a. Tính các tích vô hướng
Bài 2 (trang 45 SGK Hình học 10):
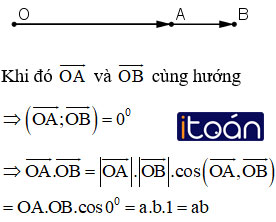
Cho ba điểm O, A, B thẳng hàng và biết OA = a, OB = b. Tính tích vô hướng 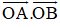
a) Điểm O nằm ngoài đoạn AB;
b) Điểm O nằm trong đoạn AB.
Hướng dẫn giải:
a) Điểm O nằm ngoài đoạn AB :
b) Điểm O nằm trong đoạn AB :
Bài 3 (trang 45 SGK Hình học 10):
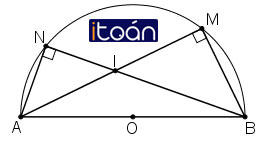
Cho nửa hình tròn tâm O có đường kính AB=2R. Gọi M và N là hai điểm thuộc nửa đường tròn sao cho hai dây cung AM và BN cắt nhau tại I.
a) Chứng minh 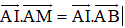
b) Hãy dùng kết quả câu a) để tính 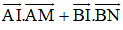
Hướng dẫn giải:
Bài 4 (trang 45 SGK Hình học 10):
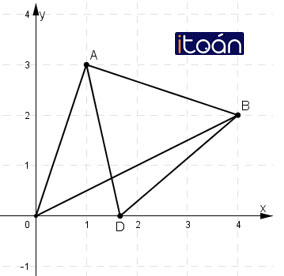
Trên mặt phẳng Oxy, cho hai điểm A(1; 3), B(4; 2).
a) Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB.
b) Tính chu vi tam giác OAB.
c) Chứng tỏ OA vuông góc với AB và từ đó tính diện tích tam giác OAB.
Hướng dẫn giải:
a) D nằm trên trục Ox nên D có tọa độ D(x ; 0)
Khi đó :
Vậy chu vi tam giác OAB là P = AO + BO + AB = √10 + 2√5 + √10 = 2√5 + 2√10
Bài 5 (trang 46 SGK Hình học 10):
Trên mặt phẳng Oxy hãy tính góc giữa hai vectơ a→ và b→ trong các trường hợp sau:
Hướng dẫn giải:
Bài 6 (trang 46 SGK Hình học 10):
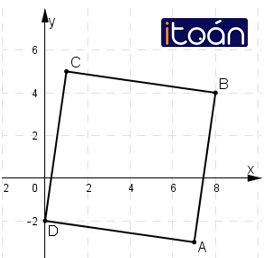
Trên mặt phẳng tọa độ Oxy cho bốn điểm: A(7; -3), B(8; 4), C(1; 5), D(0; –2). Chứng minh rằng tứ giác ABCD là hình vuông.
Hướng dẫn giải:
⇒ ABCD là hình bình hành.
⇒ hình bình hành ABCD là hình chữ nhật.
⇒ AB = AD ⇒ Hình chữ nhật ABCD là hình vuông (ĐPCM).
Bài 7 (trang 46 SGK Hình học 10):
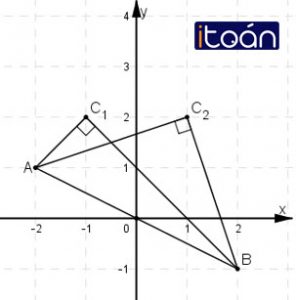
Trên mặt phẳng Oxy cho điểm A(-2; 1). Gọi B là điểm đối xứng với điểm A qua gốc tọa độ O. Tìm tọa độ của điểm C có tung độ bằng 2 sao cho tam giác vuông ở C.
Hướng dẫn giải:
B đối xứng với A qua O ⇒ O là trung điểm của AB
C có tung độ bằng 2 nên C(x; 2)
Tam giác ABC vuông tại C
Vậy có hai điểm C thỏa mãn là C1(1; 2) và C2(–1; 2).
Lời kết
Sau buổi học ngày hôm nay, các em đã nắm được lý thuyết Tích vô hướng của 2 vecto. Đồng thời, các em còn được hướng dẫn về cách vận dụng các lý thuyết vào việc giải bài tập đúng cách, nhanh chóng. Nếu các em còn thắc mắc vấn đề gì hãy liên hệ ngay với itoan để được tư vấn và giúp đỡ nhé.
Xem thêm: