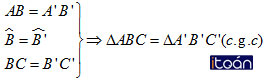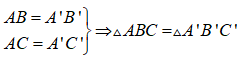Trường hợp bằng nhau thứ hai của tam giác cạnh góc cạnh – Toán 7

Trong buổi học trước, các em đã tìm hiểu về Trường hợp bằng nhau thứ nhất của tam giác cạnh cạnh cạnh. Đến buổi học này, các em sẽ cùng với itoan tiếp tục tìm hiểu về trường hợp thứ hai nha. Vậy Trường hợp bằng nhau thứ hai của tam giác cạnh góc cạnh là gì? Nó khác gì so với trường hợp thứ nhất? Hãy cùng iToan tìm hiểu nhé!

Mục tiêu bài học: Trường hợp bằng nhau thứ hai của tam giác cạnh góc cạnh

Các em hãy cùng itoan đạt được những mục tiêu sau nhé:

• Nắm các ví dụ bổ sung về Trường hợp bằng nhau thứ hai của tam giác cạnh góc cạnh.
• Nắm chắc các phương pháp làm bài tập.
• Hiểu cách giải các bài tập tự luyện để nâng cao và mở rộng kiến thức.

Lý thuyết: Trường hợp bằng nhau thứ hai của tam giác cạnh góc cạnh

1. Trường hợp cạnh – góc – cạnh

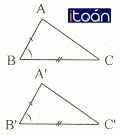
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

2. Hệ quả

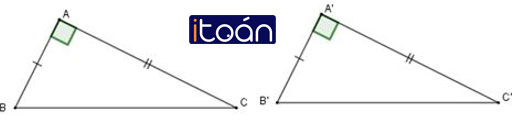
Nếu hai cạnh góc vuông của tam giác vuông này bằng hai cạnh góc vuông của tam giác kia thì hai tam giác vuông đó bằng nhau.

Cho tam giác ABC vuông tại A, tam giác A’B’C’ vuông tại A’, khi đó:

3. Ví dụ bài tập

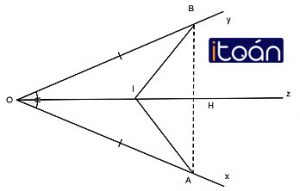
Cho góc xOy với điểm I nằm trên tia phân giác Oz, lấy điểm A trên Ox, B trên Oy sao cho OA = OB

a) Chứng minh ΔAOI = Δ BOI

b) Đoạn thẳng AB cắt Oz tại H, chứng minh rằng ΔAIH = ΔBIH

c) Chứng minh rằng ΔAHI và ΔBHI đều là tam giác vuông

Hướng dẫn giải:

a) Xét ΔAOI và Δ BOI có OI chung

Ta có: OA = OB (Giả thuyết)

∠AOI = ∠BOI (Oz là tia phân giác)

Vậy ΔAOI = Δ BOI (c-g-c)

b) Do ΔAOI = Δ BOI (c-g-c) => IA = IB (1) và ∠AIO = ∠BIO

Lại có: ∠AIH kề bù với ∠AIO, ∠BIH kề bù với ∠BOI

Suy ra ∠AIH = ∠BIH (2)

IH là cạnh chung (3)

Từ (1), (2), (3) => ΔAIH = ΔBIH

c) Ta có: ΔAIH = ΔBIH => ∠AHI = ∠BHI

Vì ∠AHI = ∠BHI và lại là góc kề bù

Suy ra ∠AHI = ∠BHI = 90⁰ 

Nên ΔAHI và ΔBHI đều là tam giác vuông tại H.

Vì bài học hôm nay rất quan trọng, nên các em cần hiểu, nắm chắc phần lý thuyết cũng như phương pháp cho từng dạng bài tập cụ thể nhé. Các em có thể xem video bài giảng dưới đây để tăng hiệu quả học tập.

Bài tập trường hợp bằng nhau thứ hai của tam giác cạnh góc cạnh

Bài 4 trang 117

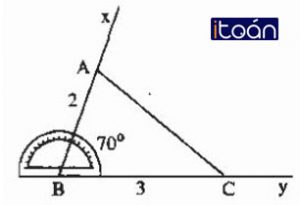
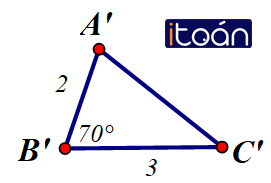
Vẽ thêm tam giác A’B’C’ có :

A’B’ = 2cm ; ∠B’ = 70^o; B’C’ = 3cm

Hãy đo để kiểm nghiệm rằng AC = A’C’. Ta có thể kết luận được tam giác ABC bằng tam giác A’B’C’ hay không?

Hướng dẫn giải bài tập:

Ta có thể kết luận được tam giác ABC bằng tam giác A’B’C’ (trường hợp cạnh – góc – cạnh)

Bài 4 trang 118:

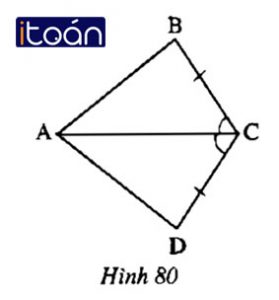
Hai tam giác trên hình 80 có bằng nhau không ? Vì sao ?

Hướng dẫn giải bài tập:

ΔABC và ΔADC có cạnh AC chung

Đồng thời, ∠ ACB = ∠ DCB, với BC = DC

⇒ ΔABC = ΔADC ( cạnh – góc – cạnh)

Bài 24 – trang 18

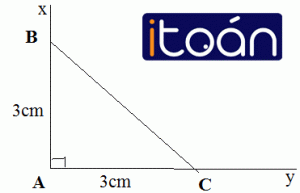
Vẽ tam giác ABC có ∠A = 90^o, AB = AC = 3cm. Sau đó đo các góc B và C.

Hướng dẫn giải bài tập:

Các em hãy lần lượt vẽ theo các bước dưới đây:

Bước 1: Vẽ ∠xAy = 90^o

Bước 2: Trên tia Ax vẽ đoạn thẳng AB = 3cm

Bước 3: Trên tia Ay vẽ đoạn thẳng AC = 3cm

Bước 4: Vẽ đoạn thẳng BC

Sau khi vẽ xong, các em sẽ được một tam giác ABC. Đây cũng chính là tam giác các em cần vẽ.  Tiếp đến, các em đo các góc B và C với ∠B = ∠C = 45º.

Bài 25 – trang 118

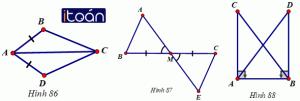
Trên mỗi hình 82, 83, 84 có các tam giác nào bằng nhau ? Vì sao?

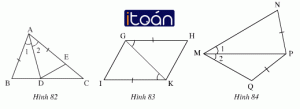
Hướng dẫn giải bài tập:

a) Hình 82: ∆ADB = ∆ADE theo trường hợp cạnh – góc – cạnh.

Giải thích: 

Ta có: AB = AE (gt)

∠A1 = ∠A2

AD là cạnh chung

b) Hình 83: ∆HGK = ∆IKG theo trường hợp cạnh – góc – cạnh.

Giải thích:

Ta có: HG = IK (gt)

∠G = ∠K

GK là cạnh chung

c) Hình 84: ∆PMQ không bằng ∆PMN

Giải thích: 

Ta có: ∠M1 = ∠M2

PM là cạnh chung

NP = QP

Nhưng góc M không phải góc xen giữa nên ∆PMQ không bằng ∆PMN

Bài 26 – trang 118

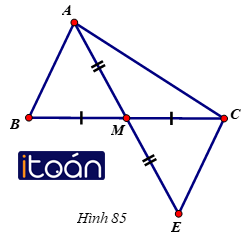
Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của MA lấy điểm E sao cho ME = MA. Chứng minh rằng AB//CE.

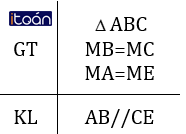
Dưới đây là hình vẽ và giả thiết kết luận của bài toán. Hãy sắp xếp lại năm câu sau đây một cách hợp lí để giải bài toán trên:

           

1. MB = MC (gt)

∠AMB = ∠EMC (đối đỉnh)

MA = ME (gt)

2) Do đó ∆ AMB = ∆ EMC (c.g.c)

3) ∠ MAB = ∠ MEC => AB // CE (có hai góc bằng nhau ở vị trí so le trong)

4) ∆ AMB = ∆ EMC => ∠ MAB = ∠ MEC (hai góc tương ứng)

5) Tam giác AMB và tam giác EMC có

Hướng dẫn giải bài tập:

Thứ tự sắp xếp là: 5, 1, 2, 4, 3, cụ thể là:

Tam giác AMB và tam giác EMC có:

• MB = MC (gt)
• ∠AMB = ∠EMC (đối đỉnh)
• MA = ME (gt)

Do đó ΔAMB = ΔEMC (c.g.c)

=> ∠MAB = ∠E (hai góc tương ứng)

=> AB // CE (hai góc so le trong bằng nhau)

Bài 27 – trang 119

Nếu thêm một điều kiện để hai tam giác trong mỗi hình vẽ dưới đây là hai tam giác bằng nhau theo trường hợp cạnh góc cạnh

a) ΔABC = ΔADC

b) ΔAMB = ΔEMC

c) ΔCAB = ΔDBA

Hướng dẫn giải bài tập:

a) Bổ sung thêm ∠BAC = ∠DAC.

b) Bổ sung thêm MA = ME.

c) Bổ sung thêm AC = BD.

Bài 28 – trang 120

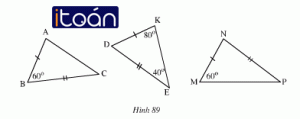
Trên hình 89 có các tam giác bằng nhau

Hướng dẫn giải bài tập:

• Trong ΔDEK có:

∠D + ∠K + ∠E = 180º

∠D + 80º + 40º = 180º

=>  ∠D = 60º

• Xét ΔABC và ΔKDE có:

AB = KD (gt)

∠B = ∠D

BC = DE (gt)

Do đó ΔABC = ΔKDE

• Xét ΔMNP và ΔABC có:

MN = AB

NP = BC

∠M = ∠B = 60º nhưng góc M và góc B không xen giữa hai cạnh bằng nhau.

⇒ ΔMNP không bằng ΔABC

⇒ ΔMNP cũng không bằng ΔKDE.

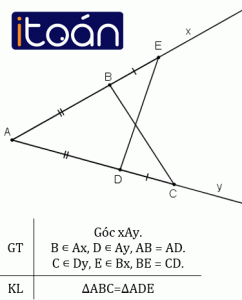
Bài 29 – trang 120

Cho ∠xAy. Lấy điểm B trên tia Ax điểm D trên tia Ay sao cho AB= AD . Trên tia Bx lấy điểm E trên tia Dy lấy điểm C sao cho BE = DC. Chứng minh rằng hai tam giác ABC và ADE bằng nhau.

Hướng dẫn giải bài tập:

Ta có: AB = AD, BE = DC ⇒ AB + BE = AD + DC hay AE = AC.

Xét ΔABC và Δ ADE có:

AC = AE (chứng minh trên)

∠A chung

AB = AD (giả thiết)

⇒ ΔABC = ΔADE (c.g.c)

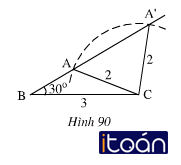
Bài 30 – trang 120

Trên hình 90, các tam giác ABC và A’BC có cạnh chung BC = 3cm, CA = CA’ = 2cm, ∠ABC = ∠A’BC=30º nhưng hai tam giác đó không bằng nhau.

Tại sao ở đây không thể áp dụng trường hợp cạnh góc cạnh để kết luận?

Hướng dẫn giải bài tập:

Góc ABC không phải là góc xen giữa hai cạnh BC và CA góc A’BC không phải là góc xen giữa hai cạnh BC và CA’. Do đó không thể sử dụng trường hợp cạnh – góc – cạnh để kết luận hai tam giác bằng nhau.

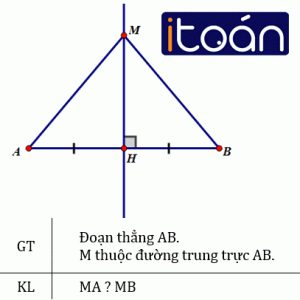
Bài 31 – trang 120

Cho đoạn thẳng AB, điểm M nằm trên đường trung trực của AB. So sánh độ dài các đoạn thẳng MA ,và MB.

Hướng dẫn giải bài tập:

Gọi H là giao điểm của đường trung trực với đoạn AB. Từ đó, ta có H là trung điểm AB và MH ⊥ AB. Xét ΔAHM và ΔBHM có:

• HM là cạnh chung.
• ∠AHM = ∠BHM (=90º)
• AH = BH (H là trung điểm AB)

Nên Δ AHM = Δ BHM

Vậy MA = MB.

Bài 32 – trang 120

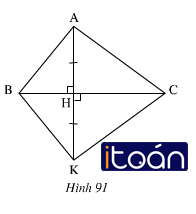
Tìm các tia phân giác trên hình 91

Hướng dẫn giải bài tập:

Ta có:

• ∠BHA = ∠CHA = 90º => HA là tia phân giác của ∠BHC.
• ∠BHK = ∠CHK = 90º => HK là tia phân giác của ∠BHC.
• Xét Δ AHM và Δ BHM có:

BH là cạnh chung

∠ AHB = ∠BHK = 90º

AH = HK

=> Δ AHB = Δ KHB (cạnh – góc – cạnh)

=> ∠ ABH = ∠ KBH (2 góc tương ứng)

=> BH là phân giác của ∠ ABK

Chứng minh tương tự, ta có: Δ AHC = Δ KHC (c.g.c)

=> ∠ ACH = ∠ KCH (2 góc tương ứng).

=> CH là tia phân giác của ∠ ACK.

Bài tập tự luyện Trường hợp bằng nhau thứ hai của tam giác cạnh góc cạnh

Bài tập 1: Cho tam giác BAC và tam giác KEF có BA = EK, ∠A = ∠K, CA = KF. Phát biểu nào sau đây đúng?

A. ΔBAC = ΔEKF

B. ΔBAC = ΔEFK

C. ΔABC = ΔFKE

D. ΔBAC = ΔKEF

Bài tập 2: Cho hình vuông ABCD, trên AB lấy điểm M, BC lấy điểm N và DC lấy P sao cho AM=BN=CP. Tính số đo góc MNP.

A. 60

B. 90

C. 100

D. A, B, C đều sai

Bài tập 3: Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C, trên tia Oy lấy hai điểm B, D sao cho OA = OB; OC = OD (A nằm giữa O và C; B nằm giữa O và D).Chọn câu đúng

A. ΔOAD = ΔOCB

B. ΔODA = ΔOBC

C. ΔAOD = ΔBCO

D. ΔOAD = ΔOBC

Bài tập 4: Cho tam giác ABC có =. Trên tia đối của tia BA lấy điểm M và trên tia đối của tia CA lấy điểm N sao cho BM = CN. Nối BN,CM. Hãy so sánh hai đoạn thẳng BN và CM.

A. BN = CM

B. BN < CM

C. BN > CM

Bài tập 5: Cho góc nhọn xOy và một điểm A nằm trong góc đó. Kẻ AH ⊥ Ox tại H và AK ⊥ Oy tại K. Kéo dài AH một đoạn HB = AH và kéo dài AK một đoạn KC = AK. Nối OA, OB, OC. Câu nào sau đây đúng:

A. OA=OB=OC

B. = 

C. A và B đều đúng

D. A đúng, B sai

Hướng dẫn giải bài tập tự luyện bài trường hợp bằng nhau thứ hai của tam giác cạnh góc cạnh

Bài tập 1: A

Bài tập 2: B

Bài tập 3: D

Bài tập 4: A

Bài tập 5: C

Lời kết

Toán hình là một trong những môn học khó nhất của chương trình lớp 7. Để học tốt môn này, các em cần tập trung nghe giảng, luyện tập giải các bài cơ bản, và làm những bài tập nâng cao thường xuyên. Nếu các em còn thắc mắc về vấn đề nào hãy liên hệ ngay với itoan để được giải đáp nhé.

Xem thêm bài giảng tại đây:

• Tam giác cân Toán 7 – Tổng hợp lý thuyết & Các dạng bài
• Cộng trừ đa thức 1 biến – Học toán 7 không khó cùng iToan
• Giá trị biểu thức đại số – Hướng dẫn giải bài tập SGK Toán 7