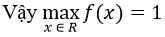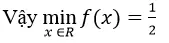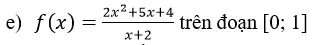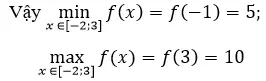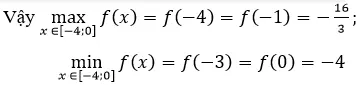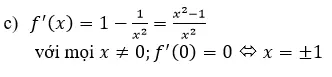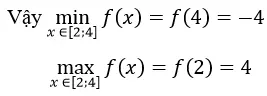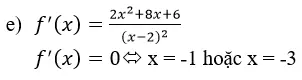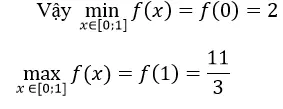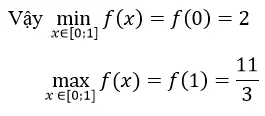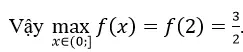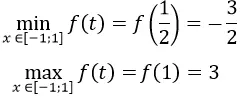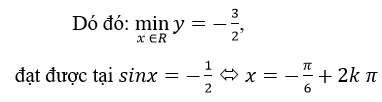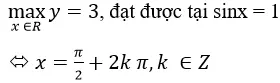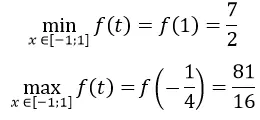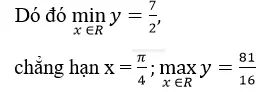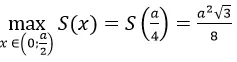Giá trị lớn nhất giá trị nhỏ nhất của hàm số – Học tốt Giải Tích 12

Chào mừng các bạn đã đến với bài giảng hôm nay của itoan. Hôm nay chúng ta sẽ học về Giá trị lớn nhất giá trị nhỏ nhất của hàm số. Nội dung bài học này sẽ giúp các em nắm được các khái niệm liên quan đến giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của hàm số trên một miền với những ví dụ minh họa sẽ giúp các em hình thành và phát triển kỹ năng giải bài tập ở dạng toán này. Cùng đến với bài học ngay thôi các bạn!

Mục tiêu bài học Giá trị lớn nhất giá trị nhỏ nhất của hàm số

• Nắm được định nghĩa giá trị lớn nhất, nhỏ nhất của hàm số.
• Nắm được phương pháp tính GTLN, GTNN của hàm số trên một đoạn, một khoảng.
• Tính được GTLN, GTNN trên một đoạn của một số hàm số thường gặp.
• Vận dụng thành thạo phương pháp tính GTLN, GTNN của một hàm số có đạo hàm trên trên một đoạn, khoảng.

Kiến thức cơ bản của bài học Giá trị lớn nhất giá trị nhỏ nhất của hàm số

I. Định nghĩa

1. Định nghĩa

Cho hàm số y=f(x)  xác định trên tập D

a. Số M được gọi là giá trị lớn nhất (GTLN) của hàm số y=f(x) trên tập D nếuf(x)≤M với mọi x thuộc  D và tồn tại x₀∈D  sao cho f(x₀)=M

Kí hiệu:  m = max_Df(x)

b. Số m  được gọi là giá trị nhỏ nhất (GTNN) của hàm số y=f(x) trên tập D nếu f(x)≥m với mọi x thuộc D và tồn tại x₀∈D sao cho f(x₀)=m

Kí hiệu:  m=min_Df(x)

2. Ví dụ

Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số trên khoảng (0;+∞):

Hướng dẫn giải:

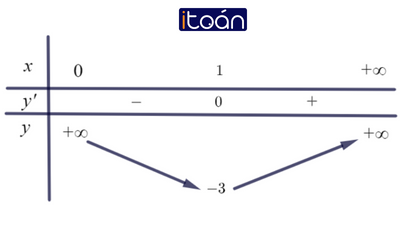
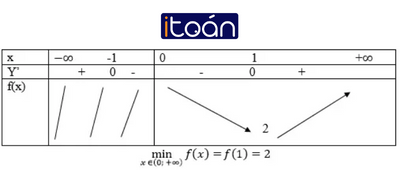
Bảng biến thiên:

Từ bảng biến thiên ta thấy trên khoảng (0;+∞) hàm số có giá trị cực tiểu duy nhất, đó cũng là giá trị nhỏ nhất của hàm số.

Vậy min f(x)=−3 (tại x=1 ), không tồn tại giá trị lớn nhất của f(x) trên khoảng (0;+∞) .

II. Cách tính giá trị lớn nhất, nhỏ nhất của hàm số trên một đoạn

1. Định lí

Mọi hàm số liên tục trên một đoạn đều có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.

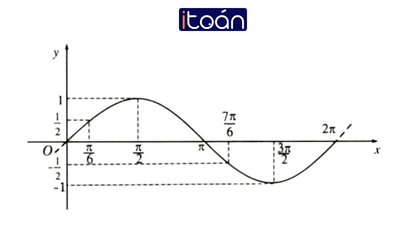
Ví dụ: Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số  y=sinx trên

2. Quy tắc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số liên tục trên một đoạn

Nhận xét

Nếu đạo hàm f′(x) giữ nguyên dấu trên đoạn [a;b]  thì hàm số đồng biến hoặc nghịch biến trên cả đoạn. Do đó, f(x)  đạt được giá trị lớn nhất và giá trị nhỏ nhất tại các giá trị đầu mút của đoạn.

Nếu chỉ có một số hữu hạn điểm x_i (x_i< x_i+1) mà tại đó f′(x) bằng 0 hoặc không xác định thì hàm số f(x) đơn điệu trên mỗi khoảng (x;x_i+1) Rõ ràng giá trị lớn nhất (giá trị nhỏ nhất) của hàm số trên đoạn là số lớn nhất (số nhỏ nhất) trong các giá trị của hàm số tại hai đầu mút a, b và tại các điểm nói trên.

Quy tắc

➀. Tìm các điểm x1,x2,...,xn  trên [a;b] mà tại đó f′(x)=0 hoặc f′(x) không xác định.

➁. Tính  f(a),f(x₁),f(x₂),…,f(x_n),f(b).

➂. Tìm số lớn nhất  M và số nhỏ nhất m trong các số trên.

Ta có M= max_[a;b] f(x)  và M=min_[a;b] f(x)

Chú ý

Hãy cùng cô xem video dưới đây để nắm rõ bài học hôm nay hơn nhé!

Hướng dẫn giải bài tập toán SGK Giá trị lớn nhất giá trị nhỏ nhất của hàm số

Để có cái nhìn tổng quan về bài học và kiểm tra kiến thức mà mình nắm được từ đầu đến bây giờ thì chúng ta hãy cùng nhau đi làm một số bài tập SGK

Bài 16 (trang 22 sgk Giải Tích 12 nâng cao) 

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: f(x) = sin⁴x+cos⁴⁡x.

Lời giải:

Hàm số xác định trên R.

Ta có f(x) = (sin²⁡⁡x )²⁡+(cos²⁡⁡x )²⁡=(sin²⁡⁡x+cos²⁡x )²⁡-2sin²⁡x.cos²⁡x=1-1/2 sin²⁡⁡2x với x ∈R.

f(x)≤1,∀x ∈R,f(0)=0.

f(x)≥1/2,∀x ∈R (do sin²2x≤1);f(π/4)=1-1/2=1/2.

Bài 17 (trang 22 sgk Giải Tích 12 nâng cao)

Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:

f(x)=x²+2x-5 trên đoạn [-2; 3]

f(x)=x³/3+2x²+3x-4 trên [-4; 0]

f(x)=x+1/x trên khoảng (0; +∞)

f(x)=-x²+2x+4 trên đoạn [2; 4]

f(x)=x-1/x trên nửa khoảng (0; 2)

Lời giải:

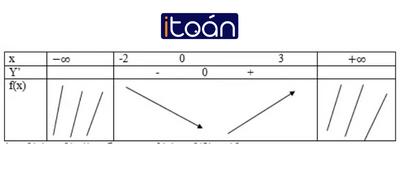
Bảng biến thiên:

Cách 2, ta có: f(-2) = -5; f(-1) = -6; f(3) = 10

f’ (x)=x²+4x+3;f’ (x)=0 <=> x = -1 hoặc x = -3

Ta có: f(-4) = -16/3;f(-3)=-4;f(-1)=-16/3;f(0)=-4

Bảng biến thiên:

Hàm số không đạt GTLN trên (0; +∞)

f’ (x)=-2x+2;f'(x)=0 <=> x = 1 (loại vì x = 1 không thuộc [2;4])

Ta có: f(2)=4;f(4)=-4

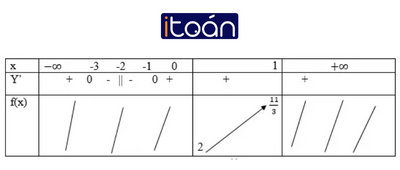
Cách 1. Bảng biến thiên:

Cách 2. Vì x ∈ [0;1] nên Phương trình f’(x) = 0 vô nghiệm trên [0; 1]

Ta có: f(0) = 2; f(1) = 11/3

f(x)=x-1/x;f'(x)=1+(1/x²) >0,∀x ∈(0;2),f(x)liên tục trên (0; 2] nên f(x) đồng biến trên (0; 2]

Hàm số không đạt giá trị nhỏ nhất trên nửa khoảng (0; 2].

Bài 18 (trang 22 sgk Giải Tích 12 nâng cao)

Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:

a) y=2 sin²⁡x+2sinx-1

b) y=cos²⁡x-sinxcosx+4

Lời giải:

Đặt t = sin x, -1≤t≤1

y=f(t)=2t²+2t-1,t ∈[-1;1]

Ta tìm giá trị lớn nhất và giá trị nhỏ nhất của y = f(t) trên [-1;1]. Đó là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên R

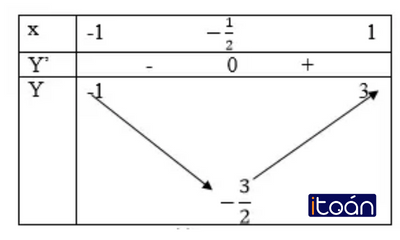
f’ (t)=4t+2,f’ (t)=0 <=> t=-1/2

Bảng biến thiên:

y=cos²x-sinxcosx+4=1-sin²2x-1/2 sin2x+4

=-sin²⁡2x-1/2 sin⁡2x+5

Đặt t = sin 2x, -1≤t≤1

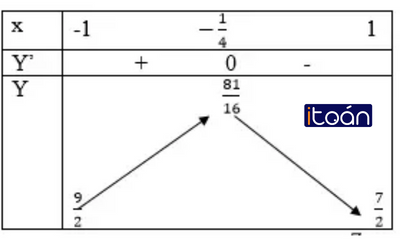
y=f(t)=-t²-1/2 t+5;f’ (t)=-2t-1/2;f’ (x)=0 <=> t=-1/4

Bảng biến thiên:

Bài 19 (trang 22 sgk Giải Tích 12 nâng cao) 

Cho tam giác đều ABC cạnh a. người ta dựng một hình chữ nhật MNPQ có cạnh MN nằm trên BC, hai đỉnh P và Q theo thứ tự nằm trên hai cạnh AC và AB của tam giác. Xác định vị trị của điểm M sao cho hình chữ nhật có diện tích lớn nhất và giá trị lớn nhất đó là.

Lời giải:

Đặt BM = x (0<x<a/2)

Ta có: MN – a – 2x; QM = BM.tan B =x √3

Diện tích hình chữ nhật MNPQ là:

S(x)=QM.MN=x √3(a-2x)

S(x)=√3(ax-2x²)

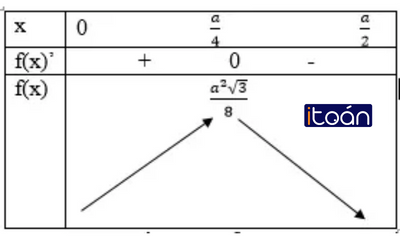
Bài toán trở thành tìm giá trị lớn nhất của S(x) trên khoảng (0; a/2)

Ta có S’ (x)=√3 (a – 4x); S’ (x) = 0 <=> x=a/4

S đạt GTLN tại x=a/4 và GTLN của diện tích hình chữ nhật MNQP là:

Bài 20 (trang 22 sgk Giải Tích 12 nâng cao)

Một hợp tác xã nuôi cá trong hồ. nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng:

P(n) = 480 – 20n (gam)

Hỏi phải thả bao nhiêu cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất?

Lời giải:

Nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì sau một vụ, số cá trên mỗi đơn vị diện tích mặt hồ trung bình cân năng:

f(n) = n – P(n) = 480n – 20n² (gam) n ∈N*

Xét hàm số f(x) = 480x – 20x² trên (0; +∞)

(Biến n lấy các giá trị nguyên dương được thay bằng biến số x lấy các giá trị trên khoảng (0; +∞))

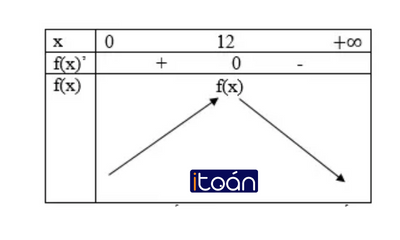
f’ (x)=480 – 40x; f’ (x)=0 <=>x = 12

Trên (0; +∞) hàm số f(x) đạt GTLN tại x = 12

Suy ra trên tập hợp N* các số nguyên dương, hàm số f đạt GTLN tại điểm n = 12.

Vậy muốn thu hoạch được nhiều cá nhất sau một vụ thì trên mỗi đơn vị diện tích của mặt hồ phải thả 12 con cá.

Kết luận

Qua bài học thú vị ngày hôm nay, các bạn cũng đã phần nào hiểu được kiến thức Giá trị lớn nhất giá trị nhỏ nhất của hàm số rồi. Bài học hôm nay chính thức kết thúc! Ngoài các kiến thức cần nhớ, các bạn có thể tự tìm hiểu nhiều bài giảng và bài tập làm thêm bổ ích khác qua trang Toán của Toppy. Tại đó các bạn sẽ được hướng dẫn học tốt chi tiết. Còn bây giờ thì chúng ta sẽ chia tay bài học tại đây nha, tạm biệt các em!

Xem thêm: 

• Đồ thị hàm số y = ax + b 
• Hàm số
• Phép chia phân số
• Biến đổi các biểu thức hữu tỉ