Đường tiệm cận – Chương trình học nâng cao Giải tích 12

Toán học kể cho ta ba câu chuyện tình buồn. Câu chuyện thứ nhất về hai đường thẳng song song chúng luôn nhìn thấy nhau nhưng không bao giờ có thể gặp được nhau. Câu chuyện thứ hai về hai đường thẳng cắt nhau rằng họ chỉ có thể gặp nhau một lần để rồi xa nhau mãi mãi. Và cuối cùng là câu chuyện của hai đường tiệm cận họ chỉ có thể càng đi càng gần nhau nhưng lại không bao giờ có điểm chung. Chúc ta cùng nhau đến với bài học về Đường tiệm cận ngay thôi nào!

Mục tiêu bài học Đường tiệm cận

Mục tiêu bài học hôm nay là gì nào, các em hãy cùng cô lập mục tiêu trước khi học bài nhé!

• Nắm vững định nghĩa tiệm cận đứng, tiệm cận ngang của đồ thị hàm số
• Biết cách tìm đường tiệm cận đứng và tiệm cận ngang
• Nhận thức được hàm phân thức hữu tỉ (không suy biến) có những đường tiệm cận nào

Kiến thức bài học Đường tiệm cận

Lý thuyết của bài học hôm nay khá dễ hiểu, các bạn chú ý ghi chép lại bài học nhé!

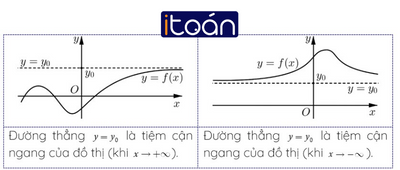
1. Đường tiệm cận ngang

Định nghĩa

Cho hàm số y=f(x) xác định trên một khoảng vô hạn (là khoảng dạng  (a;+∞),(−∞;b) hoặc (−∞;+∞)) ). Đường thẳng  y=y0 được gọi là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y=f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn

lim_x→+∞f(x)=y₀;

lim_−∞→xf(x)=y₀.

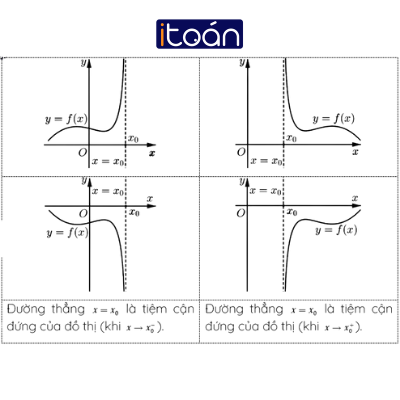
2. Đường tiệm cận đứng

Định nghĩa

Đường thẳng x=x₀ được gọi là đường tiệm cận đứng ( hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn

lim_x→x0 f(x)=+∞, lim_x→x0f(x)=−∞

📖 Lưu ý:  Với đồ thị hàm phân thức dạng như sau:

Ta luôn có

Nếu các em đã xem hết phần lý thuyết rồi mà vẫn còn băn khoăn cách làm bài tập, các em hãy cùng cô mở video để xem bài giảng của cô giáo Phạm Giang Yên Bình xinh đẹp đến từ trung tâm Toppy dưới đây nhé!

Giải bài tập SGK Đường tiệm cận

Các em chú ý làm chắc các bài tập trong sách giáo khoa nhé! Đây là phần bài tập rất sát với lý thuyết được học để vận dụng giải bài tập nâng cao hơn.

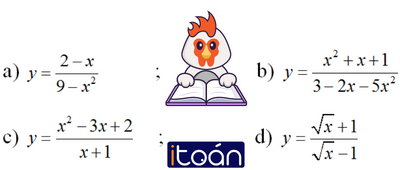
Bài 1 (trang 30 SGK Giải tích 12): Tìm các tiệm cận của đồ thị hàm số:

Lời giải

a) Ta có

⇒ Đồ thị có tiệm cận đứng là x = 2.

⇒ Đồ thị có tiệm cận ngang là y = –1.

b) Ta có:

⇒ Đồ thị có tiệm cận đứng là x = –1.

⇒ Đồ thị có tiệm cận ngang là y = –1.

⇒ Đồ thị có tiệm cận đứng là x = 2/5.

⇒ Đồ thị có tiệm cận ngang là y = 2/5.

d) Ta có:

⇒ Đồ thị có tiệm cận đứng là x = 0 (trục Ox).

⇒ Đồ thị có tiệm cận ngang là y = -1.

Bài tập tự luyện Đường tiệm cận

Phần bài tập tự luyện này cô biên soạn dành riêng cho các bạn, cùng nhau đi tìm lời giải thôi nào!

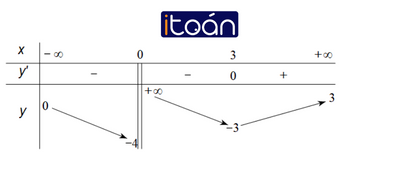
Bài tập 1: Cho hàm số y=f(x) có bảng biến thiên như sau:

Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:

A. 1

B. 3

C. 4

D. 2

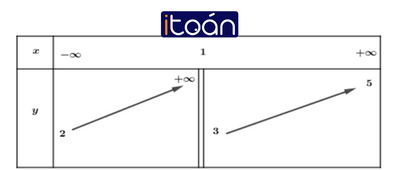
Bài tập 2: Cho hàm số y=f(x) có bảng biến thiên như sau:

Tổng số đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số đã cho là

A. 3

B. 2

C. 4

D. 1

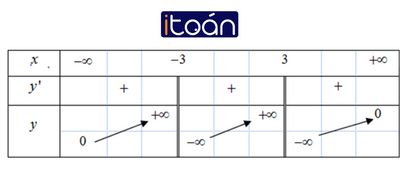
Bài tập 3: Cho hàm số y=f(x) có bảng biến thiên như sau:

Số đường tiệm cận của đồ thị hàm số là:

A. 1

B. 2

C. 3

D. 4

Đáp án

Bài tập 1: B

Bài tập 2: A

Bài tập 3: C

Lời kết:

Vậy là kết thúc bài học Đường tiệm cận rồi, các em còn vướng mắc điều gì không nhỉ? Cô rất tự hào vì các bạn đã hoàn thành rất tốt bài học hôm nay. Với những bạn muốn rèn luyện một số bài tập nâng cao có thể luyện tập thêm tại trang web Toppy với nhiều dạng bài và phương pháp hấp dẫn dành cho các bạn nhé! Xin chào và tạm biệt các em!

Xem thêm:

• Hàm số – Hướng dẫn giải bài tập
• Tổng hợp lý thuyết về hàm số 
• Kiến thức về các tập hợp số – Các dạng bài tập cơ bản
• Các kiến thức cần nhớ về hàm số bậc hai