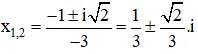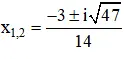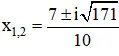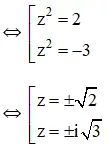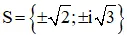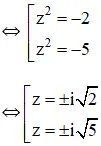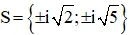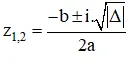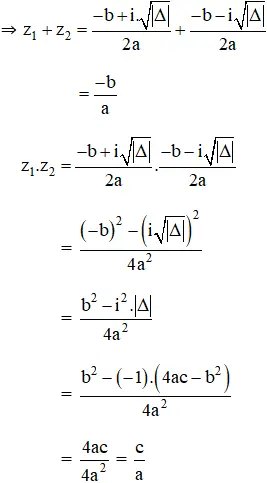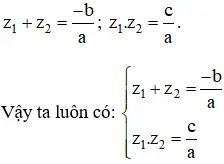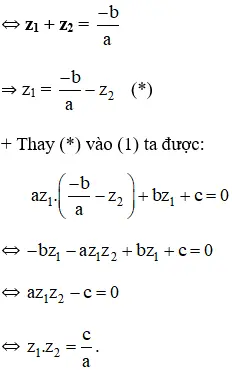Phương trình bậc hai với hệ số thực – Học tốt Giải tích 12

Sách giải toán 12 Bài 4: Phương trình bậc hai với hệ số thực giúp bạn giải các bài tập trong sách giáo khoa toán, học tốt toán 12 sẽ giúp bạn rèn luyện khả năng suy luận hợp lý và hợp logic, hình thành khả năng vận dụng kết thức toán học vào đời sống và vào các môn học khác. Bài học được itoan biên soạn rõ ràng, dễ hiểu cùng nhiều ví dụ minh họa giúp các bạn dễ dàng nắm được nội dung bài học. Hãy cùng itoan tìm hiểu thật kỹ về bài học này nhé!
Mục tiêu của bài học Phương trình bậc hai với hệ số thực
Kiến thức bài học hôm nay có đôi chút liên quan đến những bài học trước, các bạn cố gắng học tốt những bài học trước và đặt ra mục tiêu cụ thể cho bài học hôm nay nhé!
- Giúp học sinh nắm được: Căn bậc hai của một số thực âm; cách giải phương trình bậc hai với hệ số thực trong mọi trường hợp đối với Δ.
- Học sinh biết tìm được căn bậc 2 của một số thực âm và giải phương trình bậc hai với hệ số thực trong mọi trường hợp đối với Δ.
Lý thuyết bài học Phương trình bậc hai với hệ số thực
Dưới đây là một số phần kiến thức quan trọng cơ bản cô đã biên soạn cho bài học hôm nay, các bạn nhớ học bài kỹ trước khi làm bài tập nhé!
1. Căn bậc hai của số thực âm
Ví dụ: Tìm x sao cho x2=−1 ?
Vì i2=−1 nên x=±i .
Kết luận: Căn bậc hai của số thực a âm là ±i√|a|.
2. Phương trình bậc hai với hệ số thực
Phương trình bậc hai ax2+bx+c=0 (a,b,c∈′,a≠0). Xét biệt thức △=b2−4ac
Nhận xét
Trên tập hợp số phức, mọi phương trình bậc hai đều có hai nghiệm (không nhất thiết phân biệt).
Tổng quát, người ta đã chứng minh được rằng mọi phương trình bậc n(n≥1)
a0xn+a1xn−1+...+an−1x+an,0
Trong đó a0,a1,...,an∈R,a0≠0 đều có n nghiệm phức (các nghiệm không nhất thiết phân biệt).
Bài tập sách giáo khoa Phương trình bậc hai với hệ số thực
Bài tập sách giáo khoa rất sát với lý thuyết, các bạn hãy cùng itoan chinh phục các bài tập khó nhằn này nhé!
Trả lời câu hỏi Toán 12 Giải tích Bài 4 trang 139:
Thế nào là căn bậc hai của số thực dương a ?
Lời giải:
Căn bậc hai của một số thực dương a là một số thực b sao cho b2 = a.
Bài 1 (trang 140 SGK Giải tích 12):
Tìm các căn bậc hai phức của các số sau: -7;-8;-12;-20;-121
Lời giải:
Căn bậc hai của -7 là ±i √7
Căn bậc hai của -8 là ± i 2√2
Căn bậc hai của -12 là ± i2 √3
Căn bậc hai của -20 là ± i 2 √5
Căn bậc hai của -121 là ± 11i
Bài 2 (trang 140 SGK Giải tích 12):
Giải các phương trình sau trên tập hợp số phức:
a) -3z2 + 2z – 1 = 0
b) 7z2 + 3z + 2 = 0
c) 5z2 – 7z + 11 = 0
Lời giải:
a) Phương trình -3z2 + 2z – 1 = 0
có Δ’ = 12 – 3 = -2
Phương trình có hai nghiệm
b) Phương trình 7z2 + 3z + 2 = 0
có Δ = 32 – 4.7.2 = -47 < 0
⇒ Phương trình có hai nghiệm
c) Phương trình 5z2 – 7z + 11 = 0
có Δ = 72 – 4.5.11 = -171 < 0
⇒ Phương trình có hai nghiệm
Bài 3 (trang 140 SGK Giải tích 12):
Giải các phương trình sau trên tập hợp số phức:
a) z4 + z2 – 6 = 0
b) z4 + 7z2 + 10 = 0
Lời giải:
a) z4 + z2 – 6 = 0
⇔ (z2 – 2)(z2 + 3) = 0
Vậy phương trình có tập nghiệm
b) z4 + 7z2 + 10 = 0
⇔ (z2 + 2)(z2 + 5) = 0
Vậy phương trình có tập nghiệm
Bài 4 (trang 140 SGK Giải tích 12):
Cho a, b, c ∈R,a ≠ 0,z1 , z2 là hai nghiệm phân biệt ( thực hoặc phức) của phương trình ax2+bx+c=0. Hãy tính z1+z2 và z1.z2 theo hệ số a, b, c.
Lời giải:
Cách 1 :
Phương trình az2 + bz + c = 0 có Δ = b2 – 4ac
+ TH1 : Δ < 0, phương trình có hai nghiệm phức
+ TH2: Δ ≥ 0, theo định lý Vi-et ta có:
Cách 2 :
Vì z1; z2 là hai nghiệm của phương trình az2 + bz + c = 0 nên ta có:
a.z12 + bz1 + c = 0 (1)
az22 + bz2 + c = 0 (2).
+ Trừ hai vế tương ứng của (1) cho (2) ta được:
a.(z12 – z22) + b(z1 – z2) = 0
⇔ a.(z1 – z2)(z1 + z2) + b.(z1 – z2) = 0
⇔ a.(z1 + z2) + b = 0 (Vì z1 z2 nên z1 – z2 0).
Bài 5 (trang 140 SGK Giải tích 12):
Cho z = a + bi là một số phức. Hãy tìm phương trình bậc hai với hệ số thực nhận z và z− làm nghiệm.
Lời giải:
Lời kết:
Đến giờ phút này thì bài học Phương trình bậc hai với hệ số thực đến đây là kết thúc rồi, còn bạn nào có điều gì băn khoăn không nhỉ? Mỗi ngày chúng ta dành một chút thời gian đến các bài học Toán thú vị của cô sẽ giúp các bạn nâng cao kiến thức và rèn luyện tư duy tốt hơn. Ngoài ra nếu có thời gian rảnh rỗi, các bạn hãy vào trang website của Toppy, tại đây có thêm các bài tập nâng cao cho các bạn học sinh phấn đấu học lực khá giỏi. Còn bây giờ thì cô và các bạn sẽ chia tay nhau tại đây nhé! Tạm biệt!
Xem thêm bài giảng: