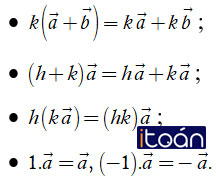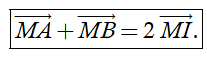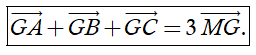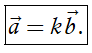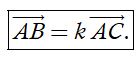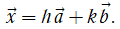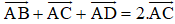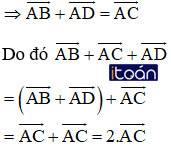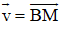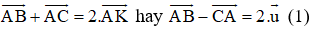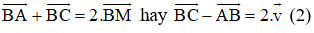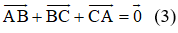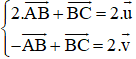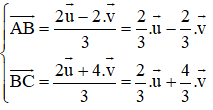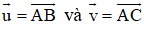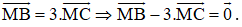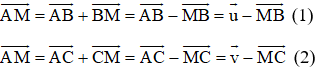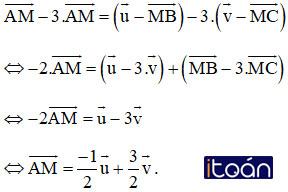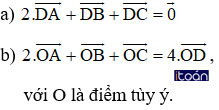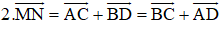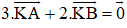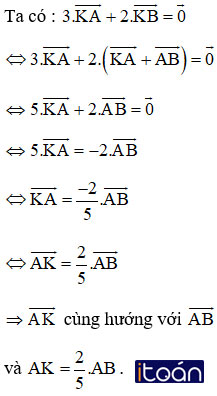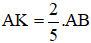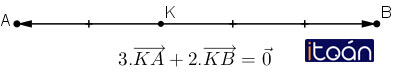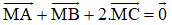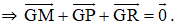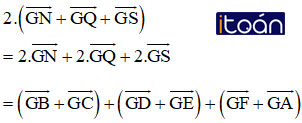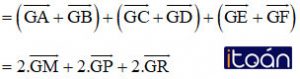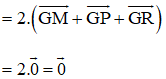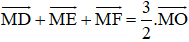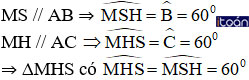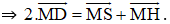Tích của Vecto với một số – Học tốt toán hình cùng itoan
Bài học Tích của Vecto với một số là một trong những kiến thức trong tâm của chương trình hình học lớp 10. Không chỉ vậy, phần kiến thức này còn đi theo các em lên lớp 11, lớp 12 và trong các đề thi. Vì vậy, các em cần phải xây dựng một nền tảng thật tốt để theo kịp với những bài toán khó hơn sau này. Nào! Bây giờ cùng lấy vở ra ghi bài và chăm chú lắng nghe itoan nhé!
Mục tiêu bài học
Trước khi đi vào bài học chính, các em hãy cùng itoan xác định mục tiêu cần đạt được sau buổi học ngày hôm nay nhé!
- Nắm chắc lý thuyết: Tích của Vecto với một số là gì?
- Nắm chắc và hiểu cách tính Tích của Vecto với một số .
- Nắm chắc phần lý thuyết của bài học. Hiểu và nắm chắc các ví dụ liên quan đến Tích của Vecto với một số . Hiểu cách giải từng dạng bài tập. Hoàn thành hết các bài tập sách giáo khoa và bài tập tự luyện để tăng khả năng nắm kiến thức.
Lý thuyết
1. Định nghĩa
Cho số k ≠ 0 và vectơ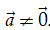 
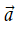
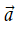
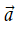
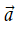
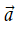
. Tích của vectơ 
với số k là một vectơ, kí hiệu là k , cùng hướng với nếu k > 0, ngược hướng với nếu k < 0 và có độ dài bằng |k|.| |
2. Tính chất
Với hai vectơ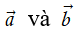 
bất kì, với mọi số h và k, ta có
3. Trung điểm của đoạn thẳng và trọng tâm của tam giác
a) Nếu I là trung điểm của đoạn thẳng AB thì với mọi điểm M thì ta có
b) Nếu G là trọng tâm của tam giác ABC thì với mọi điểm M thì ta có
4. Điều kiện để hai vectơ cùng phương
Điều kiện cần và đủ để hai vectơ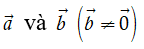 
cùng phương là có một số k để 
Nhận xét:
Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi có số k khác 0 để 
5. Phân tích một vectơ theo hai vectơ không cùng phương
Cho hai vectơ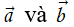 
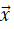
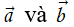
không cùng phương. Khi đó mọi vectơ 
đều phân tích được một cách duy nhất theo hai vectơ nghĩa là có duy nhất cặp số h, k sao cho 
Hướng dẫn giải bài tập sách giáo khoa
Bài 3 – 1 trang 14:
Cho vectơ a→ ≠ 0. Xác định độ dài và hướng của vectơ a→ + a→.
Hướng dẫn giải:
Ta có: a→ + a→ = 2a→
Độ dài của vecto a→ + a→ bằng 2 lần độ dài của vecto a→
Hướng của vecto a→ + a→ cùng hướng với vecto a
Bài 3 – 2 trang 14:
Tìm vectơ đối của các vectơ ka→ và 3a→ – 4b→.
Hướng dẫn giải:
Vectơ đối của các vectơ ka→ là vectơ -ka→
Vectơ đối của các vectơ 3a→ – 4b→ là vecto -3a→ + 4b→
Bài 3 trang 15:
Hãy sử dụng mục 5 của bài 2 để chứng minh các khẳng định trên.
Hướng dẫn giải:
Bài 1 (trang 17 SGK Hình học 10):
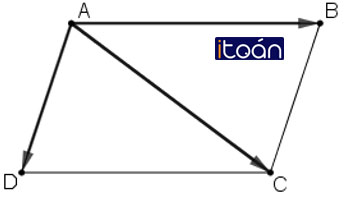
Cho hình bình hành ABCD. Chứng minh rằng: 
Hướng dẫn giải:
ABCD là hình bình hành
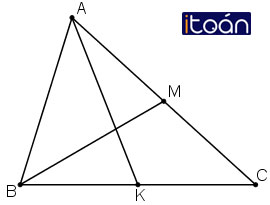
Bài 2 (trang 17 SGK Hình học 10):
Cho AK và BM là hai trung tuyến của tam giác ABC. Hãy phân tích các vectơ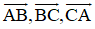 
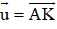
theo hai vec tơ 
và 
Hướng dẫn giải:
+ K là trung điểm của BC nên ta có: 
+ M là trung điểm AC nên ta có: 
+ Lại có 
Cộng (1) với (3) ta được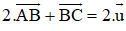 
kết hợp với (2) ta được hệ phương trình: 
Giải hệ phương trình ta được 
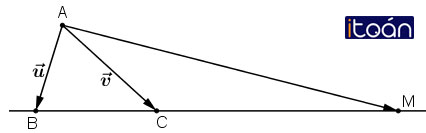
Bài 3 (trang 17 SGK Hình học 10):
Trên đường thẳng chứa cạnh BC của tam giác ABC lấy điểm M sao cho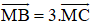 
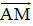
. Hãy phân tích vec tơ 
theo hai vec tơ 
Hướng dẫn giải:
Ta có: 
Theo quy tắc ba điểm ta có: 
Lấy (1) trừ 3 lần (2) ta được: 
Bài 4 (trang 17 SGK Hình học 10):
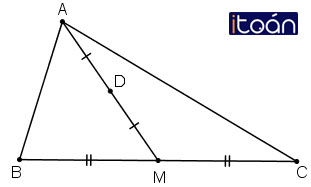
Gọi AM là trung tuyến của tam giác ABC và D là trung điểm của đoạn AM. Chứng minh rằng:
Hướng dẫn giải:
Bài 5 (trang 17 SGK Hình học 10):
Gọi M và N lần lượt là trung điểm các cạnh AB và CD của tứ giác ABCD. Chứng minh rằng: 
Hướng dẫn giải:
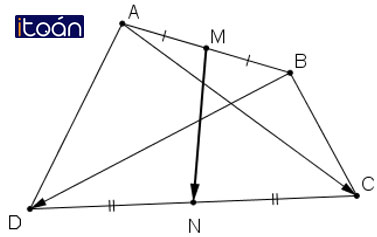
Bài 6 (trang 17 SGK Hình học 10):
Cho hai điểm phân biệt A và B. Tìm điểm K sao cho 
Hướng dẫn giải:
hay K là điểm nằm trên đoạn thẳng AB và 
Bài 7 (trang 17 SGK Hình học 10):
Cho tam giác ABC. Tìm điểm M sao cho 
Hướng dẫn giải:
Gọi D là trung điểm AB. Khi đó với mọi điểm M ta có :
⇔ M là trung điểm của trung tuyến từ đỉnh C.
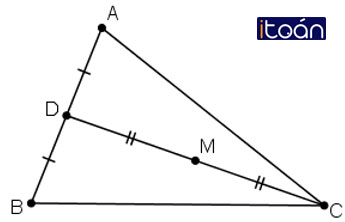
Bài 8 (trang 17 SGK Hình học 10):
Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.
Hướng dẫn giải:
Gọi G là trọng tâm tam giác MPR 
Ta cần đi chứng minh G cũng là trọng tâm của ΔNQS bằng cách chứng minh 
Thật vậy ta có:
(Vì N, Q, S lần lượt là trung điểm của BC, DE, FA)
(Vì M, P, R là trung điểm AB, CD, EF)
hay G cũng là trọng tâm của ΔNQS.
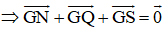
Vậy trọng tâm ΔMPR và ΔNQS trùng nhau.
Bài 9 (trang 17 SGK Hình học 10):
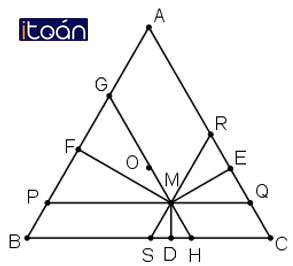
Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB.
Chứng minh rằng 
Hướng dẫn giải:
Ta có: 
⇒ ΔMHS đều.
MD ⊥ SH nên MD là đường cao đồng thời là trung tuyến của ΔMHS.
⇒ D là trung điểm của HS
Lời kết
Bài học về Tích của Vecto với một số đến đây là hết. Để nắm chắc kiến thức hơn, các em hãy xem lại video bài giảng itoan đính kèm trong phần lý thuyết. Nếu gặp khó khăn hay có vấn đề gì hãy liên hệ ngay với itoan để được các thầy cô giúp đỡ nhé! Cảm ơn các em. Chúc các em học tập thật tốt.
Xem thêm:
