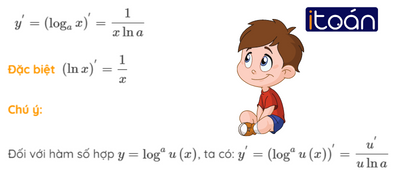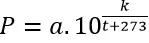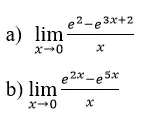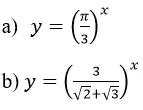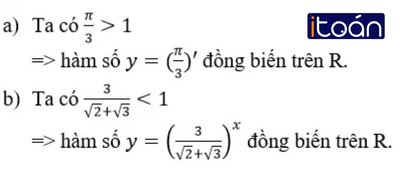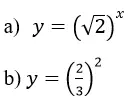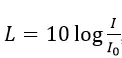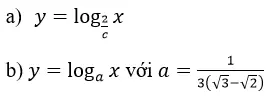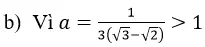Hàm số mũ Hàm số Logarit – Chinh phục giải tích 12

5/5 - (4 bình chọn)

Bài giảng Hàm số mũ Hàm số logarit hôm nay sẽ cung cấp cho các em một số dạng bài tập về biến đổi, rút gọn và đạo hàm. Bài giảng cũng giúp các em nắm rõ một số khái niệm về tính đồng biến, nghịch biến của các hàm số này. Bài soạn có hệ thống ví dụ minh họa đầy đủ về hàm số mũ, giúp cho việc ôn tập phần hàm số mũ, logarit. Vậy thì hãy cùng itoan đến với bài học hôm nay ngay thôi nào!

Mục tiêu bài học Hàm số mũ Hàm số Logarit

Sau khi học xong những bài học này, các bạn nhỏ cần nắm được các kiến thức, kĩ năng sau:

Biết khái niệm và tính chất của hàm mũ và hàm lôgarit.
Biết công thức tính đạo hàm các hàm số mũ và lôgarit và hàm số hợp của chúng.
Biết dạng đồ thị của hàm mũ và hàm lôgarit.
Biết vận dụng tính chất các hàm mũ, hàm lôgarit vào việc so sánh hai số, hai biểu
thức chứa mũ, hàm số lôgarit.
Biết vẽ đồ thị các hàm số lũy thừa, hàm số mũ và hàm số lôgarit.
Tính được đạo hàm các hàm số y = ex, y = lnx

Lý thuyết cần nắm bài Hàm số mũ Hàm số Logarit

Sau đây là những lý thuyết trọng tâm nhất được itoan biên soạn, giúp các bạn nắm vững bài học và tạo nền tảng giúp các bạn học sinh áp dụng giải các bài tập:

I. Đạo hàm của hàm số mũ

1. Định nghĩa

Cho số thực dương a khác 1. Hàm số y=a^x được gọi là hàm số mũ cơ số a.

Ví dụ:

Các hàm số sau đây là hàm số mũ y=2^x,y=(1,025)^x,y=e^x.

Hàm số y=x−5 không phải là hàm số mũ.

2. Đạo hàm của hàm số mũ

Định lý 2: Hàm số y=a^x(a>0,a≠1) có đạo hàm tại mọi x và (a^x)′=a^x.lna

Chú ý: Đối với hàm số hợp y=a^u^(x), ta có

(a^u)′=u′a^u.lna

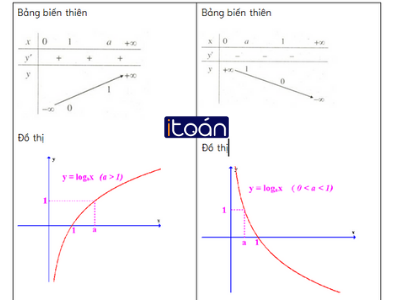
3. Khảo sát hàm số mũ y=a^x(a>0,a≠1)

Bảng tóm tắt các tính chất của hàm số mũ y=a^x(a>0,a≠1)

II. Hàm số logarit

1. Định nghĩa

Cho số thực dương a khác 1. Hàm số được gọi là hàm số lôgarit cơ số a.

Ví dụ: Các hàm số y=log₃x, y=log₁₄x, y=lnx, y=logx là các hàm số lôgarit.

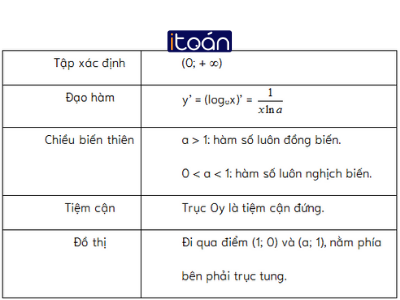
2. Đạo hàm của hàm số lôgarit

Định lý 3: Hàm số y=log_ax (a>0,a≠1) có đạo hàm tại mọi x>0 và:

3. Khảo sát hàm số mũ y=log_ax(a>0,a≠1)

Bảng tóm tắt các tính chất của hàm số logarit y=logax(a>0,a≠1)

Đạo hàm của các hàm số lũy thừa, mũ và lôgarit

Bài học này khá nhiều lý thuyết quan trọng đúng không nào, các bạn có thể kết hợp học lý thuyết cùng video hướng dẫn dưới đây để nắm chắc kiến thức hơn nhé!

Hướng dẫn giải bài tập Hàm số mũ Hàm số Logarit

Phần bài tập trong sách giáo khoa rất sát với lý thuyết nên các bạn cố gắng hoàn thành hết nhé!

Bài 47 (trang 111 sgk Giải Tích 12 nâng cao):

Khoảng 200 năm trước, hai nhà khoa học Pháp là Clô-zi-ut và Cla-pay. Trông thấy rằng áp lực P của hơi nước (tính bằng milimet thủy ngân, viết tắt mmHg) gây ra khi nó chiếm khoảng trống phía trên của mặt nước chứa trong một bình kín được tính bằng công thức

trong đó t là nhiệt đó C của nước, a và k là hằng số. cho biết k≈-2258,624.

a) Tính a biết khi nhiệt độ của nước là 40^oC (tính chính xác đến hàng phần chục)

b) Tính áp lực của hơi nước khi nhiệt độ nước là 40^oC(tính chính xác đến hàng phần chục)

Lời giải:

a) Ta có: P=760 mmHg;t=100^oC;k≈-2258,624

Bài 48 (trang 112 sgk Giải Tích 12 nâng cao):

Tìm các giới hạn sau

Lời giải:

Bài 49 (trang 112 sgk Giải Tích 12 nâng cao):

Tính đạo hàm các hàm số sau:

Lời giải:

a) y’=((x-1) e^2x)’=e^2x+(x+1)2.e^2x=e^2x (1+2x-2)=e^2x (2x-1)

Bài 50 (trang 112 sgk Giải Tích 12 nâng cao):

Trong các hàm số sau đây, hàm số nào đồng biến, hàm số nào nghịch biến trên R.

Lời giải:

Bài 51 (trang 112 sgk Giải Tích 12 nâng cao):

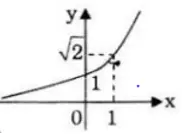
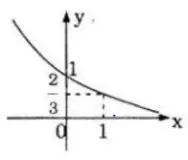
Vẽ đồ thị các hàm số sau:

Lời giải:

a) Hàm số y=(√2)^x có hệ số a=√2 > 1 => hàm số đồng biến trên R.

Với x = 0 => y = 1

Với x = 1 => y = √2

b) Hàm số y=log_2/3⁡x có a=2/3 < 1 nên hàm số nghịch biến trên (0; +∞)

Nếu x = 1 => y = 0

x=2/3 => y = 1

Bài 52 (trang 112 sgk Giải Tích 12 nâng cao):

Sử dụng công thức:

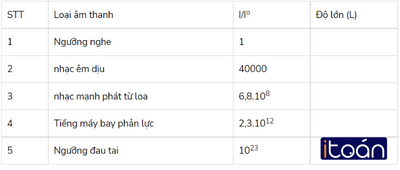
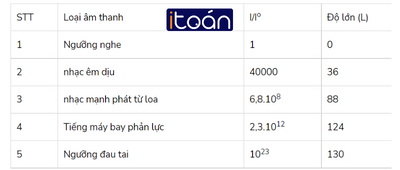
Hãy tính gần đúng, chính xác đến hàng đơn vị, độ lớn (dB) của âm thanh có tỉ số I/I_o cho trong bảng sau rồi điền vào cột trống.

Hướng dẫn giải:

Bài 55 (trang 113 sgk Giải Tích 12 nâng cao)

Trong các hàm số sau đây, hàm số nào đồng biến, hàm số nào nghịch biến trên tập xác định của nó?

Lời giải:

a) Nếu 2/c > 1 => c < 2 và c > 0 thì hàm số y=log_2/c⁡x đồng biến trên (0; +∞)

Nếu 0 < 2/c <1 <=> c > 2 thì hàm số y=log_2/c⁡x nghịch biến trên (0; +∞)

nên hàm số y=log_a⁡x đồng biến trên (0; +∞)

Lời kết sau bài học Hàm số mũ hàm số Logarit

Bài học hàm số mũ và hàm số logarit không khó đúng không các bạn? Các bạn đã nắm hết chưa nhỉ? Hy vọng với bài giảng chi tiết, dễ hiểu trên, các bạn đã nắm vững được kiến thức và áp dụng được linh hoạt trong tình huống thực tế. Ngoài ra, các bạn có thể truy cập vào trang web Toppy. Với đội ngũ giảng viên tâm huyết, nhiệt tình, Toppy luôn sẵn sàng giúp đỡ khi con gặp bất kì khó khăn nào trong học tập. Chúc các bạn luôn học tập tốt!

Xem thêm một số bài giảng liên quan khác tại đây:

Hàm số mũ Hàm số Logarit – Chinh phục giải tích 12

Mục tiêu bài học Hàm số mũ Hàm số Logarit