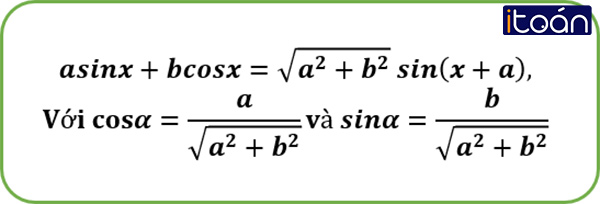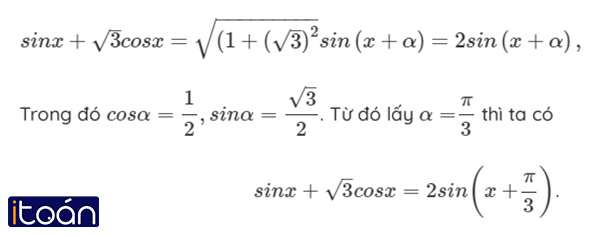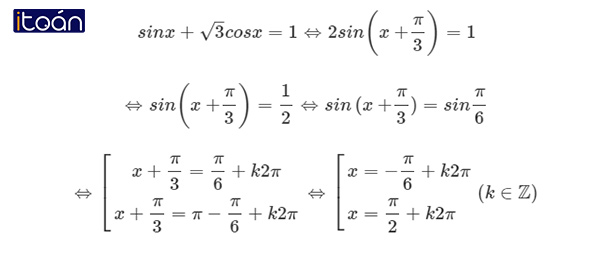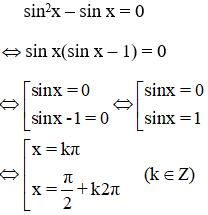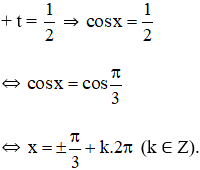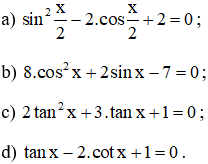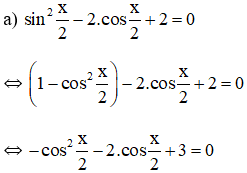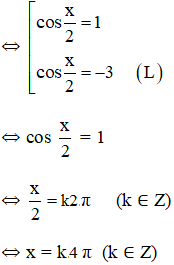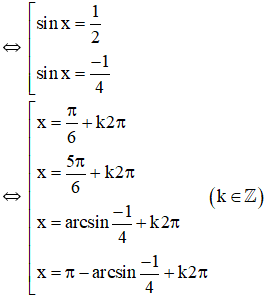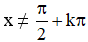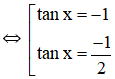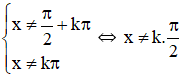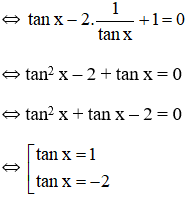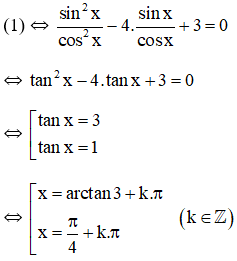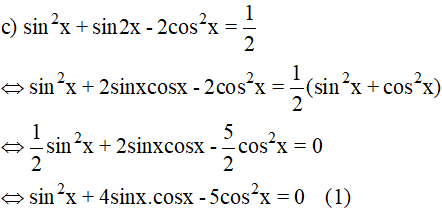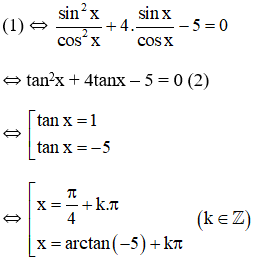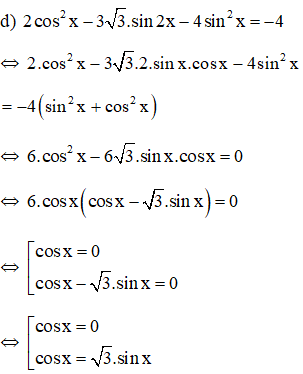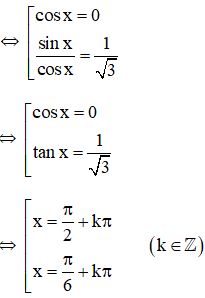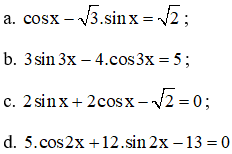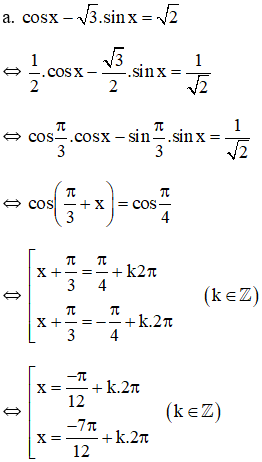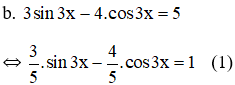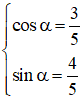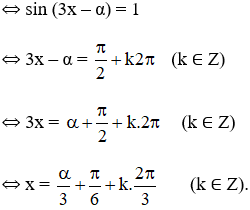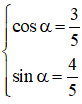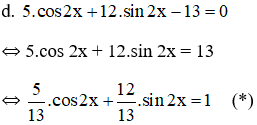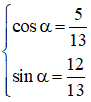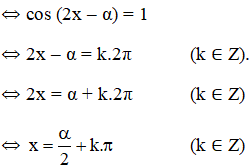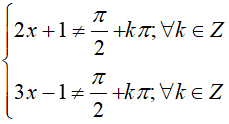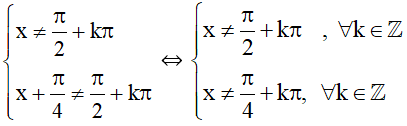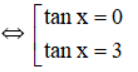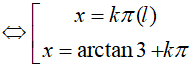Một số phương trình lượng giác thường gặp – Học tốt Đại số 11

Phương trình lượng giác là phần kiến thức quan trọng trong chương trình Đại số 11. Trong các bài trước, chúng ta đã được học về Hàm số lương giác và phương trình lượng giác. Hôm nay iToan sẽ đem đến cho các em bài học: Một số phương trình lượng giác thường gặp, do các thầy cô giáo giàu kinh nghiệm biên soạn, theo sát chương trình sách giáo khoa.
Mục tiêu bài học
Qua bài giảng này, các em cần nắm được các kiến thức sau:
- Phương trình bậc nhất, bậc hai với hàm số lượng giác
- Phương trình bậc nhất với sin x và cos x
- Hướng dẫn giải bài tập SGK
- Bài tập tự luyện
Lý thuyết cần nắm Phương trình lượng giác
Tổng hợp lý thuyết cơ bản nhất, được trình bày một cách chi tiết, giúp các em nắm được kiến thức một cách hiệu quả!
Phương trình bậc nhất đối với hàm số lượng giác
1. Định nghĩa
Phương trình bậc nhất đối với một hàm số lượng giác là phương trình có dạng
at+b=0
Với a,b là các hằng số a≠0 và t là một hàm số lượng giác nào đó.
2. Cách giải
at+b=0⇔t=−ba đưa về phương trình lượng giác cơ bản.
Ví dụ
3–√cotx−3=0⟺cotx=3–√=cotπ6
⇔x=π6+kπ,k∈Z
3. Phương trình đưa về phương trình bậc nhất đối với một hàm số lượng giác
Ví dụ: Giải các phương trình sau:
a. 5cosx−2sin2x=0;
b. 8sinxcosxcos2x=−1.
Giải
a. Ta có 5cosx−2sin2x=0⇔5cosx−4sinxcosx=0
Phương trình bậc hai đối với một hàm số lượng giác
1. Định nghĩa
Phương trình bậc hai đối với một hàm số lượng giác là phương trình có dạng
at^2+bt+c=0
Trong đó a,b,c là các hằng số (a≠0) và t là một trong các hàm số lượng giác.
2. Cách giải
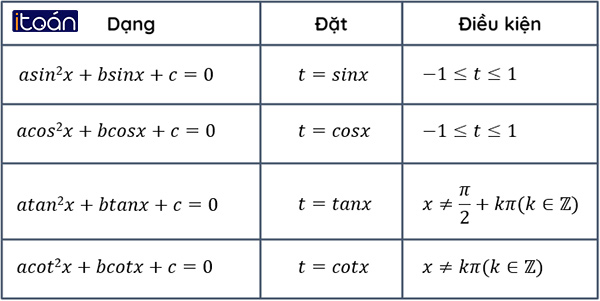
Đặt biểu thức lượng giác làm ẩn phụ và đặt điều kiện cho các ẩn phụ (nếu có) rồi giải phương trình theo ẩn phụ này. Cuối cùng, ta đưa về việc giải các phương trình lượng giác cơ bản.
Ta có bảng sau:
3. Phương trình quy về phương trình bậc hai đối với một hàm số lượng giác
Có nhiều phương trình lượng giác mà khi giải có thể đưa về phương trình bậc hai đối với một hàm số lượng giác.
Ví dụ:
Phương trình bậc nhất đối với sin x và cos x
1. Công thức biến đổi biểu thức asinx+bcosx
2. Phương trình dạng asinx+bcosx=c
- Xét phương trình asinx+bcosx=c, với a,b,c∈R;a,b không đồng thời bằng 0(a^2+b^2≠0).
- Nếu a=0,b≠0 hoặc a≠0,b=0, phương trình asinx+bcosx=c có thể đưa ngay về phương trình lượng giác cơ bản. Nếu a≠0,b≠0, ta áp dụng công thức (I).
Ví dụ: Giải phương trình
sinx+√3 cosx=1.
Giải
Theo công thức (I) ta có
Giải bài tập SGK Đại số 11 Phương trình lượng giác
Bài 1: Giải phương trình: sin2x – sin x = 0
Lời giải:
Vậy phương trình có tập nghiệm 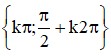
Bài 2: Giải các phương trình sau:
a) 2cos2x – 3cos x + 1 = 0
b) 2sin 2x + √2.sin4x = 0.
Lời giải:
a. 2cos2x – 3cosx + 1 = 0 (1)
đặt t = cosx, điều kiện –1 ≤ t ≤ 1
(1) trở thành 2t2 – 3t + 1 = 0
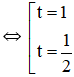
+ t = 1 ⇒ cos x = 1 ⇔ x = k.2π (k ∈ Z)
Vậy phương trình có tập nghiệm 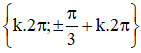
Vậy phương trình có tập nghiệm 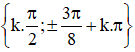
Bài 3: Giải các phương trình sau:
Lời giải:
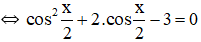
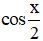
Vậy phương trình có họ nghiệm x = k4π (k ∈ Z)
b. 8cos2x + 2sinx – 7 = 0 (1)
⇔ 8(1 – sin2x) + 2sinx – 7 = 0
⇔ 8sin2x – 2sinx – 1 = 0 (Phương trình bậc hai với ẩn sin x)
Vậy phương trình có tập nghiệm {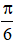
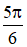
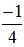
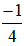
c. Điều kiện:
2tan2x + 3tanx + 1 = 0 (Phương trình bậc 2 với ẩn tan x).
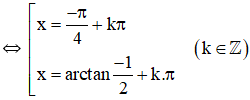
Vậy phương trình có tập nghiệm {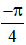
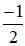
d. Điều kiện
tanx – 2.cotx + 1 = 0
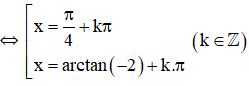
Vậy phương trình có tập nghiệm {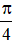
Bài 4 : Giải các phương trình sau:
a. 2sin2 x + sinx.cosx – 3cos2 x = 0
b. 3sin2 x – 4 sinx.cosx + 5 cos2 x =2
c. sin2 x + sin2x – 2 cos2 x = 1/2
d. 2cos2x – 3√3sin2x – 4sin2x = -4
Lời giải:
a) 2sin2x + sinx.cosx – 3cos2x = 0 (1)
+ Xét cos x = 0 ⇒ sin2x = 1 – cos2x = 1
Phương trình (1) trở thành: 2 = 0 (loại)
+ Xét cos x ≠ 0, chia cả hai vế của (1) cho cos2x ta được:
Vậy phương trình có tập nghiệm 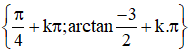
b) 3sin2x – 4sinx.cosx + 5cos2x = 2
⇔ 3sin2x – 4sinx.cosx + 5cos2x = 2(sin2x + cos2x)
⇔ sin2x – 4sinx.cosx + 3 cos2x = 0 (1)
+ Xét cosx = 0 ⇒ sin2x = 1.
Phương trình (1) trở thành 1 = 0 (Vô lý).
+ Xét cos x ≠ 0. Chia hai vế phương trình cho cos2x ta được
Vậy phương trình có tập nghiệm 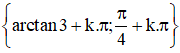
+ Xét cos x = 0 ⇒ sin2x = 1 – cos2x = 1
(1) trở thành 1 = 0 (Vô lý).
+ Xét cos x ≠ 0, chia cả hai vế cho cos2x ta được:
Vậy phương trình có tập nghiệm 
Vậy phương trình có tập nghiệm 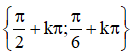
Bài 5: Giải các phương trình sau:
Lời giải:
Vậy phương trình có tập nghiệm 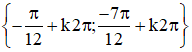
Ta có: 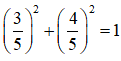
(1) trở thành: cos α.sin3x – sin α.cos 3x = 1
Vậy phương trình có họ nghiệm 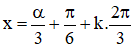
với α thỏa mãn
Vậy phương trình có tập nghiệm 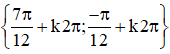
Vì 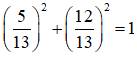
(*) ⇔ cos α.cos 2x + sin α. sin 2x = 1
Vậy phương trình có họ nghiệm 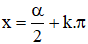
với α thỏa mãn
Bài 6: Giải các phương trình sau:
a. tan(2x + 1).tan(3x – 1) = 1
b. tanx + tan (x+π/4) = 1
Lời giải:
a. Điều kiện:
Vậy phương trình có họ nghiệm 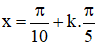
b. Điều kiện:
⇔ tan x.(1 – tanx) + tanx + 1 = 1 – tan x.
⇔ tan x – tan2x + 2.tan x = 0
⇔ tan2x – 3tanx = 0
⇔ tanx(tanx – 3) = 0
Vậy phương trình đã cho có tập nghiệm là: {arctan 3+kπ; k ∈ Z }
Bài tập tự luyện Phương trình lượng giác
Bài tập tự luyện do iToan biên soạn sẽ giúp các em luyện tập cách suy nghĩ, giải nhanh và tư duy logic!
Phần câu hỏi
Câu 1: Phương trình: 1+sin2x=0 có nghiệm là:
A. x=−π/2+k2π.
B. x=−π/4+kπ.
C. x=−π/4+k2π.
D. x=−π/2+kπ
Câu 2:
Câu 3:
Câu 4:
Phần đáp án
1.B 2.B 3.B 4.B
Lời kết
Để làm tốt các bài toán về phương trình lượng giác, các em cần hiểu và nhớ rõ tập xác định, tập nghiệm của các phương trình cơ bản. Các em có thể làm thêm nhiều bài tập tự luyên từ tự luận đến nâng cao tại Toppy. Toppy là nền tảng học trực tuyến giúp em tiết kiệm thời gian, chi phí mà vẫn học tập hiệu quả.
Chúc các em học tốt và đạt nhiều điểm cao!
>> Xem thêm:
- Phương trình đường thẳng trong không gian
- Phương trình lượng giác cơ bản cần nhớ
- Hàm số lượng giác- Đại số 11
- Tích phân- Chinh phục Giải tích 12